
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Способы задания графов
Рассмотрены два способа описания графов: графически и в виде двух множеств вершин V и ребер Е, когда каждое ребро еÎЕ определено парой инцидентных ему концевых вершин 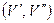 .
.
Опишем множество его вершин и ребер, а также отношение инцидентности. Занумеруем вершины графа G: V1, V2, …, Vi, Vn и ребра: е1, е2, …, еi, еm.
Отношение инцидентности задается:
1. Матрицей инцидентности 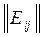 размера m x n: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i-ой вершины и j-го ребра, в случае н – графа проставляется 1, если они инцидентны и 0 – в противном случае, т.е.
размера m x n: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i-ой вершины и j-го ребра, в случае н – графа проставляется 1, если они инцидентны и 0 – в противном случае, т.е.

В случае орграфа: -1, если вершина является началом ребра;
1, если вершина является концом ребра;
0, если вершина и ребро не инцидентны.
Если некоторая вершина является для ребра началом и концом (петля), проставляется любое другое число, например, 2, т.е.

2. Списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра еiÎЕ, а в правом – инцидентные ему вершины 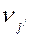 ,
,  ; для н – графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;
; для н – графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;
3. Матрицей смежности  - квадратной матрицей размера n x n; по вертикали и горизонтали перечисляются все вершины VjÎV, а на пересечении
- квадратной матрицей размера n x n; по вертикали и горизонтали перечисляются все вершины VjÎV, а на пересечении  и
и  вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины; для орграфа
вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины; для орграфа  равно числу ребер с началом в
равно числу ребер с началом в  вершине и концом в
вершине и концом в  .
.
Граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, являются изоморфными. Если два графа равны, то их матрицы совпадают.
Пример 1: Задать матрицами инцидентности и смежности, а также списком ребер графы G1, G3 (рис 2).
Матрица инцидентности:
Табл.1
| G1 | a | b | c | d | e | f | g |
| G3 | a | b | c | d | e | f | G |
| -1 | -1 | ||||||
| -1 | -1 | -1 | |||||
| -1 | |||||||
Матрица смежности:
Табл.2
| G1 | ||||
| G3 | ||||
Список ребер:
Табл. 3
| Ребро | Вершины |
| a | 1 2 |
| b | 2 1 |
| c | 1 3 |
| d | 2 3 |
| e | 2 4 |
| f | 3 4 |
| g | 4 4 |

Пример 2: Пусть дан сетевой граф:

Рис. 3
Здесь стрелки означают операции, вершины – события, характеризующие окончание одних работ и начало других. Направление стрелок отражает последовательность наступления этих событий. Задать сетевой график различными способами. Данный граф ориентированный. Может быть задан различными способами:
1) Графически (Рис 3).
2) С помощью задания двух множеств:
V = {1, 2, 3, 4, 5, 6} и Е= {(1, 2), (1, 3), (2, 5), (2, 4), (5, 6), (4, 4), (3, 4)}.
3) Матрицей инцидентности:
Табл. 4
| а (1, 2) | b (1, 3) | d (2, 4) | e (2, 5) | c (3, 4) | g (4, 6) | f (5, 6) | |
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
Особенностью графа является то, что начального события 1 только выходят, а в конечное 6 – только входят. Поэтому в первой строке единицы со знаком минус, а в последней - со знаком плюс.
4) Матрицей смежности:
Табл. 5
5) Список ребер:
Табл. 6
| ребро | Вершины |
| а | (1, 2) |
| в | (1, 3) |
| с | (3, 4) |
| d | (2, 4) |
| e | (2, 5) |
| f | (5, 6) |
| g | (4, 6) |
Пример 3: Задать различными способами графы G1, G2 (рис.4,5) соответственно.
Как вычислить число вершин и число ребер по матрицам и списку ребер? Сформировать правила переходов от описания графа списком ребер и матрице инцидентности и от матрицы смежности к списку ребер.

Матрицы инцидентности н – графа G1 и орграфа G2 приведены в таблице 7 и таблице 8. Список ребер – в таблице 9, матрицы смежности – в таблице 10.
Матрица инцидентности:
Табл. 7
| G1 | I | II | III | IV | V | VI | VII |
Табл. 8
| G2 | I | II | III | IV | V | VI | VII |
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
Списки ребер:
Табл. 9
| G1 | G2 | |||
| I, II | I, II | |||
| I, III | I, III | |||
| II, IV | II, IV | |||
| I, V | IV, II | |||
| III, IV | IV, IV | |||
| III, IV | III, V | |||
| IV, IV | III, V | |||
| III, V | III, VI | |||
| IV, VII | III, VII | |||
| V, VI | VII, VII | |||
| VI, VII |
Матрицы смежности:
Табл. 10
| G1 | I | II | III | IV | V | VI | VII | ||||||
| I | |||||||||||||
| II | |||||||||||||
| III | |||||||||||||
| IV | |||||||||||||
| V | |||||||||||||
| VI | |||||||||||||
| VII | |||||||||||||
| G2 | I | II | III | IV | V | VI | VII | ||||||
| I | |||||||||||||
| II | |||||||||||||
| III | |||||||||||||
| IV | |||||||||||||
| V | |||||||||||||
| VI | |||||||||||||
| VII | |||||||||||||
Матрица смежности н – графа симметрична относительно главной диагонали 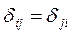 . Все ребра определяются верхним правым треугольником матрицы, расположенным над диагональю, включая последнюю. Число ребер н – графа по матрице смежности сумме элементов, расположенных на диагонали и выше, т.е. равно
. Все ребра определяются верхним правым треугольником матрицы, расположенным над диагональю, включая последнюю. Число ребер н – графа по матрице смежности сумме элементов, расположенных на диагонали и выше, т.е. равно  .
.
Ребра орграфа определяются всеми элементами  матрицы смежности, поэтому их число равно
матрицы смежности, поэтому их число равно  .
.
Список ребер графа является сокращенным представлением матрицы инцидентности (в каждой ее строке только два элемента отличны друг от 0 или один, если ребро – петля).
Построение матрицы инцидентности по списку ребер:
Каждая строка списка соответствует строке матрицы с тем же номером. Для н – графа в строке списка указаны номера элементов строки матрицы инцидентности, равные 1. Для орграфа в этой строке первым стоит номер элемента, равного 1. При совпадении номеров в строке списка ребер в названном элементе строки матрицы инцидентности проставляется, например, 2.
Построение по матрице смежности списка ребер:
Элементу матрицы, расположенному в i ой строке и j ом столбце, соответствует  строк списка ребер (при
строк списка ребер (при  = 0 ни одной строки), в каждой из которых записаны номера i и j. Для Н – графа эти строки соответствуют только элементам верхнего правого треугольника матрицы смежности, т.е. элементам
= 0 ни одной строки), в каждой из которых записаны номера i и j. Для Н – графа эти строки соответствуют только элементам верхнего правого треугольника матрицы смежности, т.е. элементам  с
с  , а для орграфа нужно рассматривать все элементы все элементы
, а для орграфа нужно рассматривать все элементы все элементы  .
.
Практическое занятие по теме: «Теория графов»
 1) Даны графы
1) Даны графы
 | |||
 |
Рис. 1
Задать граф G1, представленный на рис. 1, через множества вершин V1, и ребер Е1.
Решение: Граф G1 может быть полностью определен:
· двумя множествами – поименованных вершин 
 и поименованных ребер
и поименованных ребер  ;
;
· множеством ребер, каждое из которых представлено парой своих концевых вершин 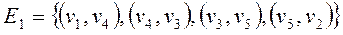 .
.
Порядок указания вершин безразличен, т.к. все ребра в графе G1 неориентированные.
2) Задать графы G2 – G3 (рис.1) множествами их вершин и рёбер. Сравнить G1 – G3.
3) Равны ли графы G1 – G2 (рис.2).
Задать графы G1 – G3 множествами их вершин и рёбер. Сравнить графы.
4) Определить дополнение  графа
графа  , если:
, если:
а) G – пятиугольник;
б) G – треугольник.
Какой ориентированный граф соответствует графу G (представить графически)?
 |  | ||||
 | |||||
|

Рис. 2
5) Даны графы
 |  | ||||
 |
Рис. 3
Определить, изоморфны ли графы G1, G2, изображенные на рис. 3.
Решение: В первом G1 и во второмG2 графах |V1| = |V2| = 5, |E1| = |E2| = 7.
Построим для этих графов матрицы инцидентности и смежности, а также список рёбер.
Матрица инцидентности:
Табл. 1
| G1 | a | b | c | d | e | F | g |
| G2 | a | b | c | d | e | F | g |
Матрица смежности:
Табл. 2
| G1 | |||||
| G2 | |||||||||||
Список рёбер:
Табл. 3
| G1 | |
| a | 1,2 |
| b | 2,2 |
| c | 2,3 |
| d | 3,3 |
| e | 3,5 |
| f | 1,4 |
| g | 4,5 |
| G2 | |
| a | 1,2 |
| b | 2,3 |
| c | 3,4 |
| d | 4,5 |
| e | 1,1 |
| f | 1,5 |
| g |
Для проверки изоморфности графов G1 и G2, например, по матрице смежности, потребуется определить, существует ли перестановка  строк и столбцов в матрице смежности G1 такая, чтобы в результате была получена матрица смежности G2.
строк и столбцов в матрице смежности G1 такая, чтобы в результате была получена матрица смежности G2.
Для проверки изоморфности графов G1 и G2 по матрице инцидентности (и списку рёбер) требуется осуществить всевозможные перестановки строк и столбцов матрицы G1, чтобы проверить, получается ли в результате пары перестановок 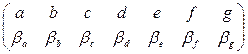 и
и  матрица инцидентности, соответствующая графу G2. Maксимальное число перестановок равно n!m! = 5!×7!, поэтому решение задачи таким способом не менее трудоемко.
матрица инцидентности, соответствующая графу G2. Maксимальное число перестановок равно n!m! = 5!×7!, поэтому решение задачи таким способом не менее трудоемко.
Однако в нашем случае по графическим представлениям G1и G2 нетрудно обнаружить сходство графов.
Для этого достаточно на рис. G2 “поднять” вершину В до условия вершин 2, 4, что позволяет обнаружить изоморфность графов.
Таким образом, графы G1 и G2 изоморфны и отличаются только нумерацией.
Нетрудно определить требуемые перенумерации вершин и рёбер графа G2, позволяющие перейти от матриц инцидентности, смежности или списка рёбер графа G1 к соответствующим представлениям графа G2:
 и
и 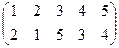 .
.
6) Задать графы G1 – G3 , изображенные на рис.1, матрицами инцидентности и смежности, а также списком ребер.
7) Задать различными способами графы G1 – G7, определённые ниже. Проверить справедливость сформулированных в примере 3 правил переходов от одного способа задания графа к другому:
а) G1 – тетраэдр;
б) G2 – тетраэдр с петлями во всех вершинах;
в) G3 – куб;
г) G4 –граф, представленный на рис.4а;
д) G5 – граф на рис.4б;
е) G6 – граф на рис.4в;
ж) G7 – граф на рис.4г.
 | |||||||
 |  | ||||||
 | |||||||
Рис. 4
8) Построить матрицы инцидентности и смежности, а также список рёбер для графа G3 (рис. 3). Изоморфен ли граф G3 графам G1 и G2 (рис.3). Проверить по матрицам смежности (или инцидентности) графов.


 9)
9)
Рис. 5
Графы (рис.5) задать матрицами смежности. Определить, изоморфны ли эти графы?

 10)
10)
Рис. 6.
Показать, что два графа (рис.6) изоморфны.
Не нашли, что искали? Воспользуйтесь поиском:
