
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нормальные формы формул алгебры логики. Совершенные нормальные формы.
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например,  является простой конъюнкцией,
является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение  является ДНФ.
является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение 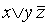 является ДНФ, но не СДНФ. Выражение
является ДНФ, но не СДНФ. Выражение  является СДНФ.
является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение  – простая дизъюнкция,
– простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение  – КНФ).
– КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение  является СКНФ.
является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:

Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)

Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
- если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 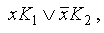 , то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
, то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
- если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например, 
или

Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ  , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
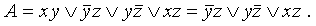
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение  ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:

г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 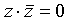 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):

Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Практическое занятие по теме: «Математическая логика»
1) Даны два высказывания:
Х: «Петров учиться в торговом институте»,
Y: 7 ≤ 5.
Определить, какие из следующих высказываний: а) 

 , б)
, б) 

 , в)
, в)  →
→ 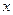 , г)
, г)  →
→  истинны, если известно, что
истинны, если известно, что 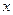 – истинное высказывание.
– истинное высказывание.
Решение:
а) 

 – истинно, т.к.
– истинно, т.к.  - истинно;
- истинно;
б) 

 – ложно, т.к.
– ложно, т.к.  - ложно;
- ложно;
в)  →
→ 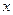 – истинно, т.к.
– истинно, т.к.  - ложно;
- ложно;
г)  →
→  – ложно, т.к
– ложно, т.к  - истинна,
- истинна,  - ложно.
- ложно.
2) Истинно или ложно высказывание (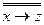 )
)  (
( (
(
 )), если Y и Х – ложные, а Z – истинное высказывание.
)), если Y и Х – ложные, а Z – истинное высказывание.
Решение:
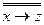 =
=  – истинно, т.к. Х – ложно
– истинно, т.к. Х – ложно 
 – истинно, т.к.
– истинно, т.к.  – ложно.
– ложно.
Значит,  (
(
 ) – истинно, значит, (
) – истинно, значит, (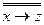 )
)  (
( (
(
 )) – истинна.
)) – истинна.
3) Какие из следующих высказываний равносильны
а)  , б)
, б)  , в)
, в) 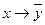 , г)
, г)  , д)
, д) 
 ?
?
Решение:  =
= 

 ,
,  =
= 

 =
= 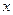

 .
.
Ответ: а) и б) равносильны;
4) Упростить схему:

Решение:
S = (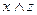 )
)  (
( ((
((

 )
)  ))) = (
))) = (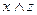 )
)  (
(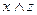 )
)  (
(

 ) =
) =
=(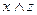 )
)  (
(

 ) =
) =  (
( (
(

 )) =
)) =  (
(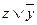 )
)  (
(

 ) =
) =  (
(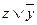 ).
).
 |
5) Студентам объявили: «в понедельник будет одна пара бухучёт и одна математика, причём, если на первой паре математики не будет, то бухучёт будет на второй паре, если третья пара не математика, то четвёртая пара бухучёт, а если математика будет на первой паре, то бухучёт на пятой паре». Определить, на какой паре будет бухучёт и на какой математика?
Решение:
Пусть х1 – математика будет на I паре;
х3 – математика будет на III паре;
y2 – бухучёт будет на II паре;
y4 – бухучёт будет на IV паре;
y5 – бухучёт будет на V паре.
S = (

 )
)  (
(
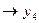 )
)  (
(
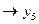 ) = ((
) = ((
 )
)  (
(
 ))
))  (
(
 ) = ((
) = ((
 )
)  (
(

 )
)  (
(
 )
)  (
(

 ))
))  (
(

 ) = ((
) = ((

 )
)  (
(

 ))
))  (
(

 ) = (
) = (



 )
)  (
(



 )
)  (
(


 )
)  (
(



 ) =
) = 




Ответ: бухучёт на II паре, математика на III паре.
6) На множестве всех действительных чисел даны два предложения (предиката):
У(х): «уравнение (относительно t)  »,
»,
Z(х):  =
=  .
.
Найти множество истинности для предложений:
а) У(х), б) Z(x), в) У(х)  Z(x), г) У(х)
Z(x), г) У(х)  Z(x).
Z(x).
Решение:
а) Уравнение  равносильно уравнению
равносильно уравнению 
 . При
. При  уравнение имеет решение. Значит, множеством истинности У(х) является множество У = (-∞; -2]
уравнение имеет решение. Значит, множеством истинности У(х) является множество У = (-∞; -2]  [2; +∞).
[2; +∞).
б)  =
= 
|  | =
| = 
 .
.  . z = (-∞; 3].
. z = (-∞; 3].
в) У(х)  Z(х):
Z(х):
 У(х)
У(х)  Z(х) = R
Z(х) = R
г) У(х)  Z(x) = (-∞; -2]
Z(x) = (-∞; -2]  [2; 3).
[2; 3).
7) Дана система уравнений:

Определить, при каких значениях 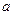 истинно каждое из следующих утверждений:
истинно каждое из следующих утверждений:
1) при любом  система имеет хотя бы одно решение,
система имеет хотя бы одно решение,
2) существует  , при котором система имеет хотя бы одно решение.
, при котором система имеет хотя бы одно решение.
Решение:
Если  , то система имеет решение при любом
, то система имеет решение при любом  ;
;
Если  , то
, то  ,
,  .
.
При  система имеет вид
система имеет вид
 Не имеет решения при
Не имеет решения при 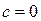 .
.
При 
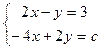 не имеет решения, например, при
не имеет решения, например, при  .
.
Итак, если  ,
,  , то система имеет решение при любом «с».
, то система имеет решение при любом «с».
Если 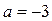 ,
,  то система имеет решение при
то система имеет решение при  .
.
Если  , то система имеет решение при
, то система имеет решение при 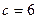 .
.
Таким образом, при любом  существует
существует  , при котором система имеет решение.
, при котором система имеет решение.
Ответ: 1)  – любое число, кроме
– любое число, кроме  ,
,  ;
;
2)  – любое число.
– любое число.
8) Упростить логическое выражение  .
.
Решение:
 .
.
9) Построить таблицу истинности:  ,
,  .
.
10) Упростить, используя свойства:  ,
,  ,
, 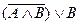 ,
,  .
.
11) Упростить:  .
.
Решение:
 .
.
12) Доказать равносильность х ~ у =  .
.
Решение:
х ~ у = 
 .
.
III. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
БИНОМ НЬЮТОНА
Не нашли, что искали? Воспользуйтесь поиском: