Полиномиальная формула.

Пусть требуется вычислить выражение , т.е. перемножив n скобок, привести его к виду

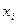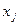Числа называются полиномиальными коэффициентами. Найдем эти числа. В соответствии с правилами алгебры из каждой скобки выбирается один из символов и они перемножаются. Коэффициенты получаются в результате приведения подобных членов в полученной таким образом сумме произведений. Таким образом коэффициент равен числу последовательностей длины n, составленных из символов , причем символ используется 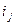раз. В соответствии с 1.1 число таких последовательностей равно 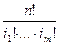. Это дает полиномиальную формулу: .

В частном случае, когда в n- ую степень возводится двучлен, она используется наиболее часто и называется биномом Ньютона

Бином Ньютона

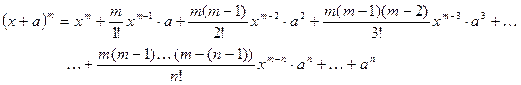
Это равенство называется формулой бинома Ньютона. Правая часть называется разложением бинома.

Свойства:

1. Показатели буквы “x” уменьшаются на 1 от первого члена к последнему, причем в первом члене показатель х равен показателю степени бинома, а в последнем 0. Показатели степени “а” увеличиваются на 1 от первого к последнему, причем в первом члене показатель при а есть 0, а в последнем он равен показателю степени бинома. Таким образом, сумма показателей степени при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.

2. Число всех членов разложения равно “m+1”, т.к. разложение содержит все степени а от 0 до m включительно.

3. Коэффициенты равны: , где n = 0, 1, 2,…, m.

4. Каждый член разложения можно получить из формулы

где n = 0, 1, 2, 3,…, m.

5. Коэффициенты членов, одинаково удаленных от концов разложения, равны между собой.

6. Т.к. коэффициенты членов равноотстоящих от концов разложения одинаковы, то наибольший коэффициент должен находиться посередине разложения. Причем, если число всех членов разложения нечетное (при четном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов четное (нечетный показатель бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами.

7. Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель “x” в этом члене и разделить на число членов, предшествующих определяемому.

8. Сумма всех биномиальных коэффициентов равна 2ⁿ. Если положить в формуле бинома , то получим .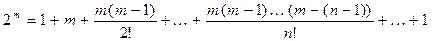

9. Если в формуле бинома “a” заменить на “–а”, то получим: , т.е. знаки “+” и ”-” чередуются.

10. Если в последнем равенстве положим , то получим: .

Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на не четных местах.

Не нашли, что искали? Воспользуйтесь поиском: