
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Применение алгоритма Дейкстры.
Фирме, занимающейся перевозкой скоропортящихся товаров, необходимо доставить товар из Суйфэньхе в Хабаровск, причем маршрутов, по которым можно произвести доставку несколько. Расстояние между Суйфэньхе и городом 2 составляет 15 км, между Суйфэньхе и городом 3 – 20 км, между Суйфэньхе и городом 11 – 85 км. Между городом 2 и городом 4 - 25 км, между городом 2 и городом 7 - 65 км. Между городом 3 и городом 5 составляет 5 км, между городом 3 и городом 8 - 50 км. Между городом 4 и городом 8 - 20 км. Между городом 5 и городом 6 - 20 км. Между городом 6 и городом 7 - 25 км, между городом 6 и городом 8 - 35 км. Между городом 7 и городом 9 - 15 км, между городом 7 и городом 10 - 40 км. Между городом 9 и городом 12 - 20 км. Между городом 10 и городом 11 - 30 км, между городом 10 и городом 12 - 45 км. Между городом 11 и городом 12 - 25 км. Требуется найти кратчайший путь из Суйфэньхе в Хабаровск
Строится граф G, в котором город Суйфэньхе обозначается цифрой 1, Хабаровск - 12. Остальные пункты маршрута обозначаются цифрами 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Каждому ребру графа сопоставляется число, которое будет равняться расстоянию между пунктами. Требуется найти минимальный маршрут. Алгоритм Дейкстры находит кратчайший путь между двумя вершинами в графе /3/. Следовательно, можно воспользоваться им, при решении данной экономической задачи.
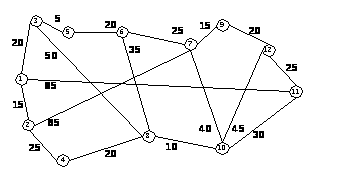
Рисунок 3– Графическая интерпретация задачи о нахождении минимального маршрута доставки
Если вершина v лежит на кратчайшем пути от начальной вершины к конечной, то T[v] – длина кратчайшего пути от начальной вершины к конечной.

С помощью алгоритма Дейкстры находится единственный минимальный маршрут, соединяющий вершины 1и 12 графа G (рисунок 3).
Пусть вершина – номер 1 – начальная вершина. Для неё назначается постоянный ярлык L(к) = 0. Конечной вершиной будет считаться вершина номер 1. Рассматриваются вершины, смежные с вершиной 12, и назначим им временные ярлыки: L(2) = 25, L(3) = 20, L(11) = 85.
Нужно выбирать вершину с самым маленьким ярлыком – это вершина номер 3, и её ярлык L(3) = 20 становится постоянным.
Повторяя этот процесс для вершины номер 3, вершинам присваиваются временные ярлыки: L(5) = 5, L(8) = 50.
Среди всех временных ярлыков минимальный будет у L(5) = 5. Этот ярлык становится постоянным.
С вершиной 5 смежна только вершина 6. L(6) = 20.
Повторяя этот процесс для вершины номер 6, вершинам присваиваются временные ярлыки: L(7) = 25, L(8) = 35.
Среди всех временных ярлыков минимальный будет у L(7) = 25. Этот ярлык становится постоянным.
Повторяя процесс, рассматриваются вершины, смежные с вершиной 7. Это 2, 9 и 10. Для которых временные ярлыки будут: L(2) = 65, L(9) = 15, L(10) = 40. Находится наименьший временный ярлык. Он будет у: L(9) = 20.
С вершиной 9 смежна только вершина 12. L(12) = 20.
Теперь, когда дерево сформировано, мы можем определить самый короткий путь от 1 до 12. Этот путь дерева, соединяющий вершины 1 и 12. И он проходит через вершины 3, 5, 6, 7 и 9. Длина этого пути - L(v') = 20 + 5 + + 20 + 25 + 15 + 20 = 105 (км.).

Рисунок 4 - Решение задачи о нахождении минимального маршрута доставки
Маршрут из города Суйфэньхе в Хабаровск, при котором время доставки товара будет наименьшим, включает город 3, город 5, город 6, город 7 и город 9.Длина маршрута составит 105 километров.
Не нашли, что искали? Воспользуйтесь поиском: