Элементы комбинаторики

На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т. д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют "комбинаторные задачи".

Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества.

Комбинаторикой называется раздел математики, изучающей вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Наиболее широкое применение комбинаторные задачи находят при решении задач теории вероятностей.

Определение. Различные группы, составленные из каких либо предметов и отличающихся одна от другой или порядком этих предметов, или самими предметами, называются соединениями. Предметы, из которых составлены соединения, называются элементами. Их обозначим а, в, с, … Соединения бывают трех родов: размещения, перестановки и сочетания.

1) Размещениями из 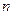элементов по называются такие соединения, из которых каждое содержит элементов, взятых из данных 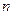элементов, и которые отличаются одно от другого или элементами, или порядком элементов .

Число всевозможных размещений, которые можно составить из n элементов по m, обозначим (А начальная буква французского слова “arrangement”, что означает размещение). Тогда .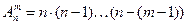

Число всевозможных размещений из n элементов по m равно произведению m последовательных целых чисел, из которых большее есть .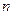

, и т.д.

Если ввести обозначение произведения от 1 до n через факториал (!), то , в частности .

Тогда число размещений равно .

Например, имеется 10 учебных предметов и 3 пары занятий в день. Тогда число способов составления расписания в 1 день равно: .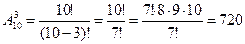

Пример: Сколько можно образовать целых чисел, из которых каждое изображалось бы тремя цифрами (номера машин)?

Решение: чисел.

Ø Размещения с повторениями: Число размещений с повторениями из 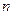элементов по задается равенством .

2) Перестановками из 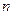элементов называются такие соединения, которые содержат все 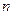элементов и отличаются друг от друга только порядком элементов. Число всех перестановок из 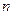элементов обозначим через P_n ( начальная буква французского слова “permutation” что означает перестановка). Тогда

Число всех перестановок из n элементов равно произведению натуральных чисел от 1 до n.

Например, число способов размещения 12 студентов за столом, на котором поставлено 12 приборов равно: .

Ø Перестановки с повторениями: Пусть дано множество из n элементов, в котором n₁ элементов принадлежит к первому типу, n₂ ко второму типу и т.д. до n_k объектов k ^го типа, причем элементы одного и того же типа не различимы между собой. Тогда общее число перестановок данного множества 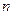элементов равно:

, где .

Пример: Сколько различных способов можно образовать из всех букв слова “Миссисипи”?

Решение: .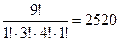

3) Сочетаниями из 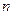элементов по называются такие соединения, которые содержат элементов и отличаются друг от друга хотя бы одним элементом. Число всех сочетаний из 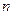элементов по равно ( начальная буква французского слова “combinaison” что значит сочетание).

Например, из 10 кандидатов на одну и ту же должность должны быть выбраны трое. Тогда число способов выбора равно: .

Свойство сочетаний: .

Правило Паскаля: .

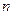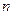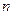Ø Сочетания с повторениями: Сочетаниями из элементов по с повторениями называются неупорядоченные выборы из предметов по с возвращениями. Число сочетаний из элементов по с повторениями равно

, можно доказать .

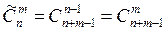Ø Принцип умножения: Пусть необходимо выполнить одно за другим, какие то действий. Если первое действие можно выполнить n₁ способами, после чего второе действие можно выполнить n₂ способами и т.д. до k ^го действия, которое можно выполнить n_k способами, то все действий вместе могут быть выполнены 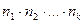способами.

Пример: Сколько четырехзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5.

Решение:

.

Ø Принцип сложения: Если два действия взаимно исключают одно другое, причем одно из них можно выполнить n₁ способами, то какое либо одно из них можно выполнить (n₁+n₂) способами. Этот принцип легко обобщить на случай произвольного конечного количества действий.

Пример: В нашем распоряжении есть 3 различных флага. На флагштоке поднимается сигнал, состоящий не менее чем из 2 флагов. Сколько различных способов сигналов можно поднять на флагштоке, если порядок флагов в сигнале учитывается?

Решение: Пусть первым действием поднимем на флагшток 2 флага, а вторым действием поднимем 3 флага. По принципу умножения 2 флага можно поднять

способами. Аналогично поднять 3 флага можно 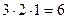способами. Мы можем поднять только один сигнал из 2 флагов, либо сигнал из 3 флагов. Эти действия взаимно исключаются, не могут быть выполнены одновременно. Тогда общее количество сигналов равно .

Практическое занятие №1 по теме: «Элементы комбинаторики.»

1) Упростить выражение .

Решение: .

2) Упростить выражение .

Решение: .

3) При расследовании хищения установлено, что у преступника семизначный телефонный номер, в котором ни одна цифра не повторяется. Следователь, полагая, что набор этих номеров потребует одного – двух часов, доложил о раскрытии преступления. Прав ли он?

Решение: Телефонный номер обычно не начинается с “0”. Значит, вычислим число комбинаций из девяти различных цифр по 7. Это размещение.

номеров.

Если на проверку тратить 1 мин на 1 номер, то на всё уйдет 3 024 часа или 126 суток. Следователь, значит, не прав.

4) Сколькими способами семь разных учебников можно поставить на полке в один ряд?

Решение: P₇ = 7! = 5040 способов.

5) В штате прокуратуры областного центра, имеется 5 следователей. Сколькими способами можно выбрать двух из них для проверки оперативной информации о готовящемся преступлении?

Решение: способами.

6) В розыгрыше первенства по футболу среди вузов принимает участие 16 команд, при это любые две команды играют между собой только один матч. Сколько всего календарных игр?

Решение: игр.

7) В телефонном номере преступника встречаются только цифры 2, 4, 5, 7 семизначного телефонного номера. Сколько всего вариантов?

Решение: В семизначном номере встречаются только 4 цифры, остальные 3 повторяют какие-то из имеющихся. Следовательно, имеет задачу о размещениях из 4 цифр по семи, т.е. с повторениями.

16384 номера.

8) Сколькими способами можно разложить в ряд две зелёные и 4 красные папки?

Решение: Число способов разложения равно числу перестановок с повторениями.

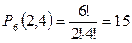способов.

9) Сколькими способами можно переставит буквы в слове “какао”, чтобы получились всевозможные различные наборы букв?

Решение: В заданном слове – 5 букв, причем “и” и “a” повторяются по два раза, а “o” встречается один раз.

Тогда способов.

10) В кондитерской имеется пять разных видов пирожных. Сколькими способами можно выбрать набор из четырёх пирожных?

Решение: Можно выбрать как различные вида пирожных, так и повторяющиеся и даже составить набор из четырёх одинаковых пирожных. Порядок следования пирожных в наборе не имеет значения. Значит, будет число сочетаний с повторениями.

символов.

Не нашли, что искали? Воспользуйтесь поиском: