
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача коммивояжера. Коммивояжер желает посетить 6 городов
Коммивояжер желает посетить 6 городов. Они соединены сетью дорог
Расстояние между городом 1 и городом 2 составляет 6 км, между городом 1 и городом 3 - 7 км, между городом 1 и городом 4 - 20 км, между городом 1 и городом 5 - 12 км, между городом 1 и городом 6 - 10 км. Расстояние между городом 2 и городом 3 составляет 5 км, между городом 2 и городом 4 - 7 км, между городом 2 и городом 5 - 9 км, между городом 2 и городом 6 - 16 км. Расстояние между городом 3 и городом 4 составляет 4 км, между городом 3 и городом 5 - 10 км, между городом 3 и городом 6 - 12 км. Расстояние между городом 4 и городом 5 составляет 3 км, между городом 4 и городом 6 - 15 км. Расстояние между городом 5 и городом 4 составляет 6 км, между городом 5 и городом 6 - 4 км, между городом 6 и городом 3 - 11 км, между городом 6 и городом 5 - 21 км. Коммивояжёр должен посетить все 6 городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным
Данную задачу можно решить венгерским методом, методом совершенного паросочетания. Для этого требуется построить матрицу А, отображающую длину между городами: aij – расстояние от города i до города j (i ≠ j), если i = j, то ставится ∞,так как дороги не существует.

Строится приведенная матрица с целью получения в каждой строке и столбце не меньше одного кратчайшего маршрута (нулевого приведенного значения). Для этого в каждой строке матрицы А от каждого элемента отнимается значение минимального элемента этой строки:

Вычисляется коэффициент приведения, равный сумме всех минимальных элементов матрицы А, которые вычитали из строк и столбцов:
Кпр = 6 +5 + 4 + 3 + 4 + 10 = 32
Вычисляются коэффициенты значимости для каждого занулившегося элемента, где aij – элементы приведенной матрицы.

К12 = 1 + 1 = 2
К23 = 2
К34 = 1 + 2 = 3
К45 = 5 К61 = 2
К56 = 2 + 4 = 6
Из приведенной матрицы нужно вычеркнуть строку и столбец, содержащие элемент с максимальным коэффициентом значимости. В данном случае таким элементом является а56: коэффициент значимости равен 6. Для элемента а56 установим значение1: а56 = 1.
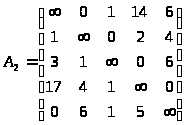
Коэффициент значимости:
К12 = 2
К23 = 2
К45 = 5
К61 = 2
К34 = 3
5) а45 = 1
Коэффициент значимости:
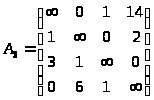
К12 = 2
К61 = 2
К34 = 3
К23 = 2
а45 = 1
Коэффициент значимости:
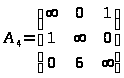
К12 = 7
К61 = 7
К23 = 2
а12 = 1, а61 = 1
а23 = 1
Таким образом, в маршрут вошли ребра: {5,6}, {4,5}, {3,4}, {1,2}, {6,1}, {2,3}. Все вершины (города) соединились. Длина маршрута составляет w({5,6}) + w({4,5}) + w({3,4}) +w({1,2}) + w({2,3}) = 4 + 3 + 4 + 6 + 10 + 5 = 32. Путь коммивояжера включает расстояния между городами {1,2},{2,3},{3,4},{4,5},{5,6},{6,1}, и имеет длину 32.
Не нашли, что искали? Воспользуйтесь поиском: