Практическое занятие по теме: «Теория множеств».

1) Определить множество А решений уравнения х² – 25 = 0.

Решение: А = { х | х² - 25 = 0 } = { -5; 5 }.

2) Определить множество В решений неравенства 2х + 9 0.

Решение: В = { х | 2х + 9 0 } = { х | х -4,5 } = [ -4,5; ∞).

3) Заданы множества А = { 1; 3; 4; 6 } и В = { 3; 5; 6; 7 }. Определить результаты операций А В, А В, А\В, В\А, А+В.

Решение:

А + В = (А\В) (В\А)

диаграмма Эйлера-Винна.

А В = { 1; 3; 4; 5; 6; 7 };

А В = { 3; 6 };

А\В = { 1; 4 };

В\А = { 5; 7 };

А + В = { 1; 4; 5; 7 }.

4) Определить результаты тех же операций, если А = { х | 1 х 5 }, В = { х | 3 х < 7 }.

Решение:

А В = { х | 3 х 5 } = [ 3; 5 ];

А В = { х | 1 х < 7 } = [ 1; 7);

А\В = { х | 1 х < 3 } = [ 1; 3);

В\А = { х | 5 < х < 7 } = (5; 7);

А + В = { х | 1 х < 3 5 < 4 < 7 } = [ 1; 3) (5; 7).

5) Доказать формулу В (А\В) = А В.

Решение: Рассмотрим диаграммы

А\В:

В (А\В):

Результат для правой части:

А В:

Оба рисунка полностью совпадают, что требовалось доказать.

6) Найти все подмножества множества А = { 0; 1; 3 }.

Решение: Несобственные подмножества Ø и А; одноэлементные {0}, {1}, {3}; двухэлементные {0; 1}, {0; 3}, {1; 3}. Следовательно, степень множества Р(А), т.е. множество всех подмножеств, имеет вид Р(А) = {Ø; {0}; {1}; {3}; {0; 1}; {0; 3}; {1; 3}; {0; 1; 3}}.

Проверка: если множество А состоит из ″n″ элементов, то число всех его подмножеств равно .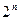

В нашем случае, n = 3. Значит, 2³ = 8, что совпадает с числом объектов в Р(А).

7) Оценить множество А = {2; 6; 1; 8}.

Решение: max А = 8, min A = 1, sup A = 8, inf A = 1.

8) Оценить множество N = {1; 2; 3; …}, т.е. натуральный ряд.

Решение: min N = 1, max N – не существует, sup N – не существует, inf N = 1.

9) Оценить множество А = { х | 2 ≤ х < 5 }.

Решение:

min А = 2, max A –не существует, т.к. 5 А, sup A = 5, inf A = 2.

10) Оценить множество А = { х | 3 < х < 8 }

Решение:

min A – не существует, т.к. 3 А, max А – не существует,

inf A = 3, sup A = не существует (sup A = ∞).

II. МАТЕМАТИЧЕСКАЯ ЛОГИКА

Основные понятия

Не нашли, что искали? Воспользуйтесь поиском: