Теоретические сведения. Преподавание данного курса имеет практическую направленность и проводится в тесной взаимосвязи с другими общепрофессиональными дисциплинами

Введение

Преподавание данного курса имеет практическую направленность и проводится в тесной взаимосвязи с другими общепрофессиональными дисциплинами. Использование межпредметных связей обеспечивает преемственность изучения материала.

Материал данного предмета используется при изучении дисциплин “Математика и информатика”, “Математическая статистика”, “Архитектура ЭВМ, систем и сетей”, “Основы алгоритмизации и программирование”, “Базы данных”, “Автоматизированные системы”, “Технология разработки программных продуктов”, “Компьютерное моделирование”.

Рабочей программой дисциплины предусматривается изучение:

· основ теории множеств;

· основ теории графов;

· основ комбинаторики;

· основ алгебры логики.

В результате изучения дисциплины студент должен:

иметь представление:

· о значении и областях применения данной дисциплины:

знать:

· основы теории множеств;

· аппарат формул логики и теорию булевых функций;

· основы алгебры вычетов;

· основные формулы комбинаторики;

· основы теории графов;

уметь:

· выполнять операции над множествами, применять аппарат теории множеств для решения задач;

· строить таблицы истинности для формул логики и упрощать формулы логики;

· представлять булевы функции в виде форму заданного типа, определять возможность выражения одних булевых функций через другие;

· исследовать бинарные отношения на заданные свойства;

· выполнять операции в алгебре вычетов;

· применять простейшие шифры для шифрования текстов;

· находить характеристики графов, выделять структурные особенности графов, исследовать графы на заданные свойства, применять аппарат теории графов для решения прикладных задач;

Базовыми дисциплинами для изучения предмета “Дискретная математика” являются “Математика” и “Информатика”.

Теоретические сведения

I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

Понятие множества

Под множеством понимается совокупность некоторых объектов. Эти объекты, предметы называются элементами множества. Множества будем обозначать А, В, С,…, или А₁, А₂,… Если множество состоит из конечного числа элементов, то оно называется конечным. Например, множество студентов в группе конечное. Если количество элементов множества бесконечное, то оно называется бесконечным. Например, множество всех натуральных чисел бесконечное. Множество всех прямых, проходящих через одну точку на плоскости, бесконечное.

Конечному множеству относятся множество, не содержащее ни одного элемента (пустое множество). Число элементов пустого множества равно нулю .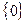

Если элемент х принадлежит множеству А, то 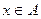; если нет-то .

Определение 1. Если каждый элемент множества А есть элемент множества В, то А является частью или подмножеством множества В: 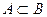при этом .

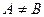В частности, 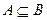, если А=В, т.е. множество А есть подмножество самого себя. Кроме того, пустое множество есть часть всего множества. Множество А и пустое множество называются несобственными подмножествами множества А, все остальные называются собственными. Если множество содержит 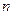элементов, то подмножеств будет .

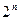Определение 2. Суммой (объединением) двух множеств А и В называется множество, элементы которого принадлежат хотя бы к одному из множеств. Обозначаются .

Если множеств несколько, то имеем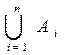

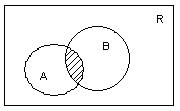
Объединение множеств А и В можно изобразить диаграммой Эйлера – Винна

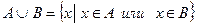
Определение 3. Произведением (пересесечением) двух множеств А и В называется множество, элементами которого являются общие элементы обоих множеств:

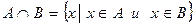
Если множеств несколько, то запишем .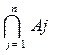

Определение 4. Разностью множеств А и В называется множество тех элементов множества А, которые не суть элементы множества В: А \ В.

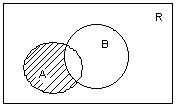
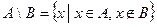
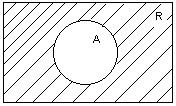
Определение 5. Дополнением 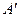множества называется

.

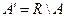Свойства

1. Коммутативность: ;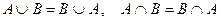

2. Ассоциативность:

,

;

3. Дистрибутивность (пересечения относительно объединения)

.

В общем случае

,

,

.

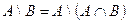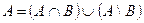Очевидны следующие соотношения двойственности (сложения и пересечения). Для любой (конечной или бесконечной) системы подмножеств А_j данного произвольного множества Х имеет место тождества

.

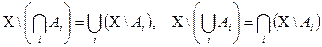Последовательность множеств М₁, М₂, …, М_n, … называется убывающей (возрастающей), если для любого 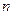имеем .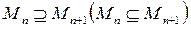

Замечание. Пересечение (сумма) любой бесконечной подпоследовательности совпадает с пересечением (суммой) всей последовательности.

Сумма разностей множеств: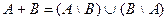

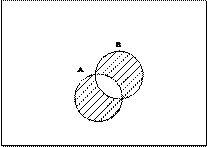
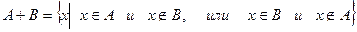
Бинарные отношения

Пусть даны два множества А и В. Множество упорядоченных пар элементов, из которых первый принадлежит А, а второй В, называется бинарным (декартовым) произведением множеств А и В и обозначается АхВ.

Пример:

Всякое подмножество множества АхВ называется бинарным отношением.

Пример: , .

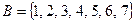Для отношения R элемент 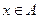есть делитель элемента 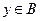имеем

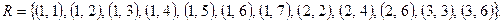
Бинарные отношения можно задавать различными способами: таблицами, стрелками, сечениями. Для табличного способа представления отношения проводят несколько вертикалей, обозначая каждую из них некоторым элементом из А, и несколько горизонталей, обозначая их элементами из В. Затем жирными точками отмечают пересечения тех прямых, для которых соответствующие элементы удовлетворяют отношению R.

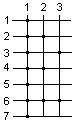
Для того чтобы задать стрелочное представление бинарного отношения 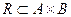, элементы А и В изображаются в виде точек плоскости, после чего стрелками, направленными от х к у, соединяются те и только те 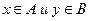, для которых .

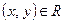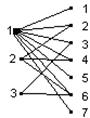
Поскольку А есть подмножество В, можно условится не обозначать два раза точки 1, 2, 3, представляющие один и тот же элемент; тогда получим

Не нашли, что искали? Воспользуйтесь поиском: