Операции над множествами.

Основные понятия и определения теории множеств. Мощность множества.

Под множеством А мы понимаем совокупность объектов произвольной природы, объединенных общим свойством Р(х).

Множество из двух элементов (0,1) – поле. Поле Галуа – GF(2) = P₂

Обозначение

1) Указанием определяющего свойства A = { x | P(x) }

2) Перечислением элементов A = { x₁, x₂, …, x_n }

Основные понятия:

1) пустое множество, обычно обозначается символом Ø (в нем совсем ничего нет);

2) подмножество (множество, элементы которого являются элементами множества, которому принадлежит подмножество) и надмножество (множество элементов множества, которые не вошли в подмноество);

3) пространство (универсальное множество – множество вообще всевозможных элемнтов);

Мощность множества – количество элементов в множестве.

| A | = n

Принцип включения и исключения

Принципом включения и исключения называется формула, позволяющая вычислить мощность объединения множеств, если известны их мощности и мощности всех пересечений.

Рассмотрим частные случаи этой формулы для двух и трех множеств:

Справедливы аналогичные формулы и для пересечения множеств:

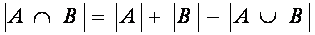
Операции над множествами.

· пересечение – когда «х» и в одном и в другом множестве

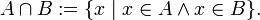
· объединение – когда «х» либо в одном либо в другом множествах

Если множества A и B не пересекаются: , то их объединение обозначают также: .

· разность (дополнение) – когда «х» только в А но не в В

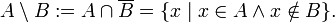
· Декартово или прямое произведение – перемножение всевозможных пар элементов

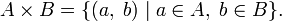
Покрытие множества – семейство множеств, такое, что их объедение дает исходное множество.

Разбиение множества – представление множества в виде непересекающихся элементов.

Количество разбиений – полиномиальный коэффициент:

ПОЛЕ – множество с двумя внутренними ассоциативными и коммутативными бинарными операциями, связанными законом дистрибутивности. По первой операции есть нейтральный и обратный элементы для каждого. По второй операции – есть нейтральный для каждого кроме нейтрального по первой операции. (пример: Поле действительных чисел с операциями сложения и умножения)

Поле из конечного числа элементы – поле Галуа (французский математик ^_^)

GF(2) – поле из 2 элементов.

Не нашли, что искали? Воспользуйтесь поиском: