Понятие вектора. Линейные операции над векторами.

Вектором наз. упорядоченная совокупность чисел Х={X₁,X₂,...X_n} вектор дан в n-мерном пространстве. Т(X₁,X₂,X₃). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.

Линейные операции над векторами обладают следующими свойствами:

1. а+b=b+а

2. (а +b) +с=а + (b +с),

3. λ1 • (λ2 •а) =λ1 •λ2 •а,

4. (λ1 +λ2) •а =λ1 •а +λ2 •а,

5. λ • (а +b) =λ •а+λ •b.

15. Координаты вектора.

На плоскости координаты вектора v относительно данного базиса (a, b) – это такая пара чисел (x; y), что v = x a + y b. Любой вектор имеет однозначно определенные координаты относительно любого базиса.

При сложении векторов складываются их соответственные координаты; при умножении вектора на число каждая координата умножается на это число. Скалярное произведение векторов с координатами (x; y) и (x'; y') равно сумме произведений соответственных координат: xx' + yy'.

Чтобы вычислить координаты вектора 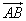, зная координаты (x ₁; y ₁) его начала A и координаты (x ₂; y ₂) его конца B, нужно из координат конца вычесть координаты начала: (x ₂ – x ₁; y ₂ – y ₁).

Все сказанное справедливо и для случая пространства с той разницей, что базис в пространстве состоит из трех векторов, а наборы координат векторов и точек – из трех чисел.

16..Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

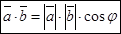
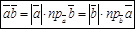
1.

2.

3.

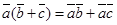
4.

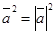
5.

Не нашли, что искали? Воспользуйтесь поиском: