Гиперболические поверхности

Гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

(однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

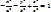(двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двухполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP − BP | = const. В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

29. Гипербола. Определение. Вывод канонического уравнения.

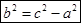
Не нашли, что искали? Воспользуйтесь поиском: