
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Достататочное условие существования экстремума.
Пусть функция y = f(x) непрерывна на всем интервале (a, b), дифференцируема на (a, b), кроме, быть может, числа x0(a,b), причем точка (x0, f(x0)) является критической точкой графика функции f. Тогда, если при переходе через x0 производная меняет знак с плюса на минус (с минуса на плюс), то f'(x0) – максимум (минимум) функции f.
Доказательство.
Пусть при переходе через x0 производная функции f меняет знак с плюса на минус. Рассмотрим x = x0 + Δx(a,b) число. Если Δx > 0, то, воспользовавшись теоремой Лагранжа, имеем f(x)- f(  )=f’’(ζ)(x-x0)<0 где ζ
)=f’’(ζ)(x-x0)<0 где ζ  (x0,x) т.е. f(x)<f(x0), если Δx < 0, то f(x0)-f(x)=f’’(ζ)(x0-x)>0, где ζ
(x0,x) т.е. f(x)<f(x0), если Δx < 0, то f(x0)-f(x)=f’’(ζ)(x0-x)>0, где ζ  (x0,x),т.е. f(x0)>f(x)
(x0,x),т.е. f(x0)>f(x)
Доказано, что значение f(x0) – максимум функции f. Аналогично доказывается, что если при переходе через x0 производная меняет знак с минуса на плюс, то f(x0) – минимум функции f.
Теорема доказана.
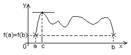
47. Теорема Роля: если функция f(x) непрерывна на заданном промежутке [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует точка с из интервала (a,b), такая, что f’(c)=0.
48. Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа 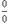 или
или  .
.
Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если 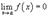 и
и 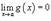 , то
, то 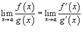 ;
;
· Если  и
и 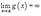 , то аналогично
, то аналогично 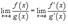 .
.
Формула Телора
Тейлора формула, формула

изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:
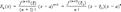
Не нашли, что искали? Воспользуйтесь поиском: