
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производная суммы и частного.
Производная произведения функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо 
Производная частного функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

| 52. Теорема Коши |
Если функции f (х) и  (х) непрерывны на отрезке [ а, b ] и дифференцируемы в интервале (а, b), причем (х) непрерывны на отрезке [ а, b ] и дифференцируемы в интервале (а, b), причем  , то существует точка сÎ (а,b) такая, что , то существует точка сÎ (а,b) такая, что
 Доказательство. Рассмотрим функцию
F (х) = [ f (х) -f (а)] –
Доказательство. Рассмотрим функцию
F (х) = [ f (х) -f (а)] –  . [ . [ 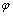 (х) - (х) - 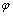 (а)].
Легко проверить, что эта функция удовлетворяет теореме Ролля (аналогично тому, как это было сделано в предыдущей теореме). Следовательно, существует точка сÎ (a, b.) такая, что (а)].
Легко проверить, что эта функция удовлетворяет теореме Ролля (аналогично тому, как это было сделано в предыдущей теореме). Следовательно, существует точка сÎ (a, b.) такая, что   . .  Отсюда получаем утверждение теоремы.
Замечание.
Равенства
Отсюда получаем утверждение теоремы.
Замечание.
Равенства  и и
 называются соответственно формулами Лагранжа и Коши.
54.Теорема Лагранжа.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0. называются соответственно формулами Лагранжа и Коши.
54.Теорема Лагранжа.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.


|
55. Необходимое условие существования точки перегиба:
если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то  .
.
Достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и  , и
, и  при
при  , а
, а  , то функция f(x) имеет в x0 точку перегиба.
, то функция f(x) имеет в x0 точку перегиба.
Не нашли, что искали? Воспользуйтесь поиском: