Выпуклость и вогнутость линий точки перегиба.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.

Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0

Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х₀

Асимптоты.

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при:

Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

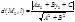
Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

существует предел:

Не нашли, что искали? Воспользуйтесь поиском: