Выражение скалярного произведения через координаты( перемножаемых векторов)

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Теорема: Скалярное произведение двух векторов a =(x₁,y₁,z₁) и вектора b =(x₂,y₂,z₂)

Выражается формулой: (a, b)= x₁x₂+ y₁y₂+ z₁z₂

Длинна вектора

| a |=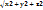

Приложение скалярного произведения

cosϕ

Замечание: в координатной форме необходимым и достаточным условием является выполнение условия.

18. Векторное произведение векторов и его свойства.

Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую.

Векторным произведением вектора 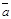на вектор называется вектор , который:

1. Перпендикулярен векторам 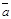и .

2. Имеет длину, численно равную площади параллелограмма, образованного на векторах 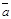и .

, где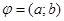

3. Векторы 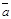, и образуют правую тройку векторов.

Свойства:

1.

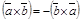
2.

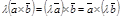
3.

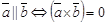
4.

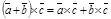
19. выражение векторного произведения через координаты

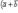
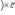
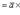
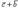
3) (распределительное свойство).

Выражение векторного произведения 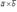через проекции векторов и на координатные оси прямоугольной системы координат дается формулой

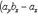
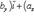
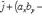
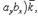(27)

которую можно записать с помощью определителя

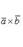
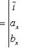
(28)

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

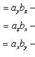
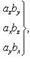(29)

и тогда на основании (4)

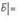
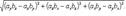(30)

Механический смысл векторного произведения состоит в следующем: если вектор - сила, а вектор есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы 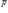относительно точки O есть вектор, равный векторному произведению радиуса-вектора 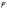точки приложения силы на силу , т. е.

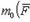
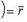
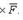
20. Смешанное произведение векторов и его свойства.

Смешанное произведение записывают в виде: .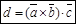

Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами.

Свойства.

1. Смешанное произведение не меняется при циклической перестановке сомножителей:

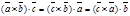
2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.

4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

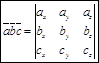
Три вектора называются компланарными, если результат смешанного произведения равен нулю.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: