Интервал и радиус сходимости. Рассмотрим функцию . Ее областью определения является множество тех значений x, при которых ряд сходится

Рассмотрим функцию 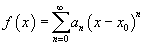. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.

Если интервал сходимости представляется в виде 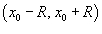, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера:

Множество значений «икс», при котором степенной ряд сходиться называется областью сходимости ряда.

Для любого степенного ряда возможны три случая:

1) Степенной ряд сходится абсолютно на некотором интервале если любое значение «икс» из интервала будет давать абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости:

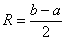
Геометрически ситуация выглядит так:

В данном случае, интервал сходимости ряда: 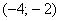, радиус сходимости ряда: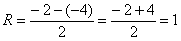

Широко распространен случай, когда интервал сходимости симметричен относительно нуля:

>

Здесь интервал сходимости ряда: 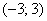, радиус сходимости ряда:

В точках x=a, x=b степенной ряд может, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. Найти области сходимости ряда:

– Если степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: (a;b)

– Если степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: [a;b) или (a;b].

– Если степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: [a;b]

2) Степенной ряд сходится абсолютно при любом значении x. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 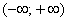. Радиус сходимости: .

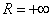3) Степенной ряд сходится в единственной точке.

Если ряд имеет вид 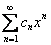, то он сходиться в единственной точке x=0. В этом случае интервал сходимости и область сходимости ряда совпадают и равны – нулю: x=0.

Если ряд имеет вид 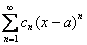, то он сходиться в единственной точке x=a,

если ряд имеет вид 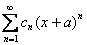, то он сходиться в единственной точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: R=0.

Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал (a;b) (возможно полуинтервал, отрезок). L анная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.

Не нашли, что искали? Воспользуйтесь поиском: