Предельные признаки сравнения рядов

Пусть даны два ряда и 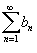, у которых члены a_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

· Если , то оба ряда и 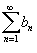либо сходятся, либо расходятся;

· Если , то ряд сходится, если сходится ряд ;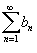

· Если , то ряд расходится, если расходится ряд .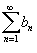

Так называемый обобщенный гармонический ряд сходится при p > 1 и расходится при 0 < p≤ 1.

Признак Даламбера

Пусть − ряд с положительными членами. Тогда справедливы следующие свойства:

 Если , то ряд сходится;

 Если , то ряд расходится;

 Если , то ряд может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.

Не нашли, что искали? Воспользуйтесь поиском: