Определение ряда Фурье

Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2 π. В этом случае достаточно рассмотреть поведение функции в интервале [ −π, π ].
Предположим, что функция f (x) с периодом 2 π абсолютно интегрируема в интервале [ −π, π ]. При этом является конечным так называемый интеграл Дирихле:

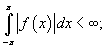
1. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).

Если x ₀ − точка разрыва, то ряд Фурье сходится к значению

Ряд Фурье функции f (x) представляется в виде

где коэффициенты Фурье a ₀, a_n и b_n определяются формулами

Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя a_n и b_n новыми переменными d_n и φ_n или d_n и θ_n, где

можно, соответственно, записать

Не нашли, что искали? Воспользуйтесь поиском: