Геометрический смысл теоремы Лагранжа

На кривой 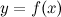между точками и найдется точка , такая, что через эту точку можно провести касательную, параллельную хорде .

Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:

Вопрос 16.

Теорема Коши. (Об отношении конечных приращений двух функций)

Если функци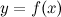и и :

1. непрерывны на отрезке ;

2. дифференцируемы на интервале ;

3. производная на интервале ,

тогда на этом интервале найдется по крайней мере одна точка 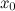, такая, что

Вопрос 19.

Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I.

Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.

Вопрос 20.

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка 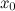называется точкой строгого локального максимума функции 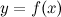, если для всех из окрестности этой точки будет справедливо строгое неравенство .

Точка 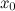называется точкой строгого локального минимума функции 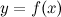, если для всех из окрестности этой точки будет справедливо строгое неравенство .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание:

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Не нашли, что искали? Воспользуйтесь поиском: