Схема исследования функции на выпуклость, вогнутость

1. Найти вторую производную функции.

2. Найти точки, в которых вторая производная равна нулю или не существует.

3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Вопрос 23.

Асимптоты – это значение к которому функция будет стремится, но некогда его не пересечёт

Вертикальные асимптоты параллельны оси Оy.

Горизонтальные асимптоты параллельны оси Оx и находятся при помощи предела:

Наклонные асимптоты записываются уравнением прямой с угловым коэффициентом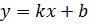

Вопрос 25.

Численное решение уравнений и их систем состоит в приближённом определении корней уравнения или системы уравнений и применяется в случаях, когда точный метод решения неизвестен или трудоёмок.

Поделим отрезок [a,b] пополам точкой c, координата которой c=(a+b)/2 и вычислим значение функции f(c).

Возможны два случая:

а) f(a) f(c)>0, т.е. значения функции на концах отрезка [a, c] одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b] и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c: a=c; f(a)=f(c);

б) f(a) f(c)<0, т.е. значение функции на концах отрезка [a, c] противоположны по знаку; тогда корень находится на отрезке [a, c] и отрезок [c, b] можно исключить из дальнейшего рассмотрения, перенеся точку b в точку c: b=c.

После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала [a, b] не станет меньше некоторой заданной малой величины 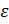, т.е. |b-a| < 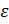, и тогда любое значение аргумента из отрезка [a, b] можно считать корнем с погрешностью 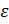. Обычно принимают в качестве корня середину отрезка.

Отметим, что 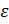здесь имеет смысл допустимой абсолютной погрешности вычисления корня.

Достоинством метода является его безусловная сходимость, если на интервале [a, b] имеется хотя бы один корень. Кроме того, метод не использует производных. К недостаткам относят медленную сходимость, т.е. достаточно большое число вычислений функции f(x) по сравнению с другими методами. Рекомендуется к использованию в тех случаях, если нет жестких требований ко времени счета.

Вопрос 26.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 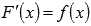для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 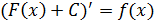. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.
Производная результата интегрирования равна подынтегральной функции.

2.
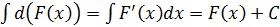
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. , где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.

4.
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Вопрос 29.

Пусть функция F(X) задана на отрезке [ А, B ]. Разобьем от­резок [ А, B ] на П произвольных частей точками:

Выберем в каждом из частичных отрезков [ Xi, Xi+1 ] произволь­ную точку ξ I:

Теперь образуем сумму произведений:

Которую будем называть Интегральной суммой для функции F (X) на отрезке [ А, b ]. Геометрический смысл величины σ: это сумма площадей прямоугольников с основаниями Δ Xi и высотами F (ξ I) (I = 1, 2,..., П).

Введем еще одну величину. Обозначим через λ длину максимального частичного отрезка данного разбиения:

Определение.

Конечный предел I интегральной суммы σ при λ → 0, если он существует, называется Определенным интег­ралом от функции F (X) по отрезку [ А, B ]:

Если F(x) – первообразная подынтегральной f(x), а f(x) непрерывна на [a,b], то

*- Формула Ньютона - Лейбница

1.

2.

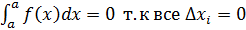
3.

4.

5.

Вывод формулы Ньютона-Лейбница:

подставим a

Следовательно:

Вопрос 32.

Геометрический смысл определенного интеграла. Если f (x) непрерывна и положительна на [ a, b ], то интеграл

представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x)

Площадь фигуры, ограниченной осью Ох, двумя вертикальными прямыми х=а, х=b и графиком функции f(x), определяется по формуле:

Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции.

Вопрос 33.

Теорема 1.

Объем прямого кругового конуса с высотой Н и радиусом основания R

Объём вычисляется по формулам:

1.

2. V = ¹/₃ π R²H

Вопрос 34

Определённый интеграл называется несобственным интегралом, если выполняется, по крайней мере одно из следующих условий – предел а или b (или оба предела) являются бесконечными; функция f (x) имеет одну или несколько точек разрыва внутри интервала [a,b].

Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся. В противном случае интегралы расходятся.

Если для некоторого действительного числа c оба интеграла в правой части сходятся, то говорят, что интеграл также сходится.

Пусть f(x) и g(x) являются непрерывными функциями в интервале [a,∞). Предположим, что для всех x в интервале [a,∞).

1. Если f(x) сходится, то g(x) также сходится

2. Если g(x) расходится, то f(x) также расходится

3. Если |f(x)| сходится, то f(x) также сходится. В этом случае говорят, что интеграл f(x) является абсолютно сходящимся.

Вопрос 35.

Метод трапеций является одним из методов численного интегрирования. Он позволяет вычислять определенные интегралы с заранее заданной степенью точности.

Не нашли, что искали? Воспользуйтесь поиском: