Статистическая оценка вероятности события.

При этом вводится понятие относительной частоты появления события A, равной отношению , где m – число испытаний, в которых произошло событие А; n – общее число испытаний.

Я. Бернулли доказал, что при неограниченном увеличении числа испытаний относительная частота события А будет сколь угодно мало отличать от вероятности события А.

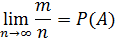
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события A есть отношение меры A (длины, площади, объема) к мере U пространства элементарных событий.

Свойства вероятности:

1. Вероятность случайного события А находится между 0 и 1.

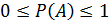
2. Вероятность достоверного события равно 1.

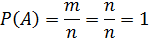
3. Вероятность невозможного события равна 0.

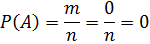
Вопрос 55.

События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого

События называются совместными, если в результате данного испытания появление одного из них исключает появление другого.

Теорема сложения вероятностей:

Теорема:

Вероятность суммы двух несовместных событий А и B равна сумме вероятностей этих событий:

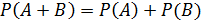
Теорема:

Вероятность суммы конечного числа попарно несовместных событий 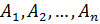равна сумме вероятностей этих событий, т.е.

Из этой теоремы можно вывести два следствия:

Следствие 1.

Если события 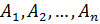образуют полную группу, то сумма их вероятностей равна единице, т.е.

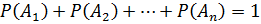
Следствие 2.

Сумма вероятностей противоположенных событий равна единице, т.е.

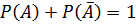
Теорема:

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т.е.

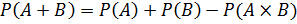
Вопрос 56.

Событие А называется независимым от события B, если вероятность осуществления события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если его вероятность меняется в зависимости от того, произошло событие В или нет.

В случае зависимых событий А и В вводится понятие условной вероятности, под которой понимается вероятность события А при условии, что событие В произошло. Обозначается P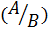

Теорема:

Вероятность произведения 2 независимых событий А и В равна произведению вероятностей этих событий:

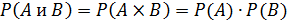
Теорема:

Вероятность произведения двух зависимых событий А и В равна произведению одного из них на условную вероятность второго, вычислительную при условии, что первое событие осуществилось.

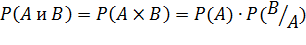
Теорема:

Вероятность появления хотя бы одного из событий 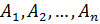, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположенных событий 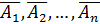, т.е.

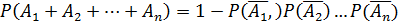
Вопрос 57.

Теорема:

Вероятность события В, которое может наступить при условии появления одного из событий 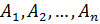, образующих полную группу попарно несовместных событий, рана сумме произведений вероятностей каждого из событий 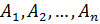на соответствующую условную вероятность события В

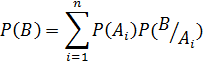
Полученная формула называется формулой полной вероятности, а события 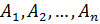– гипотезами.

С формулой полной вероятности тесно связана формула Байеса. Формула Байеса позволяет переоценить вероятность гипотез после того, как в результате опыта произошло событие B.

Вопрос 58.

Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.

Обозначим эти вероятности как p и q. Исход с вероятностью p будем называть “успехом”, а исход с вероятностью q – “неудачей”.

Формула Бернулли:

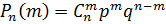
где

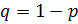
Так как рассматривалась только одна из возможных комбинаций, когда событие A произошло только в первых m испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из n элементов по m, т.е.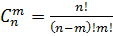

Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний n. При больших значениях n пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.

Теорема. Если вероятность 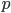наступления события 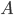в каждом испытании постоянна и мала, а число независимых испытаний 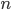достаточно велико, то вероятность наступления события 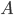ровно 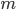раз приближенно равна

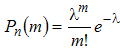
где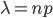

Вопрос 59.

Дискретной называют такую случайную величину, которая принимает счетное множество значений, т.е. такое множество, элементы которого можно подсчитать.

Распределением (законом) случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими им вероятностями.

Распределение дискретной случайной величины может быть задано в виде таблицы, в графическом и аналитическом виде.

Функция распределения определяет вероятность того, что случайная величина X принимает значение, меньшее фиксированного действительного числа x, т.е.

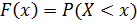
Функцию F(x) можно получить, суммируя значения вероятностей по тем значениям случайной величины, которые меньше 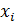, т.е.

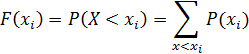
Вопрос 60.

Математическое ожидание характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.

Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных её значений на соответствующие вероятности:

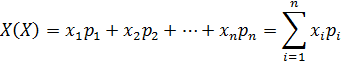
Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно этой постоянной:

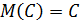
2. Постоянный множитель можно выносить за знак математического ожидания:

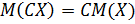
3. Математическое ожидание математической суммы случайных величин равно алгебраической сумме их математических ожиданий:

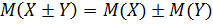
Две случайные величины Х и Y называются независимыми, если распределение одной из них не зависит от того, какое значение приняла другая величина.

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

5. Математическое ожидание отклонения случайной величины от её математического ожидания всегда рано нулю:

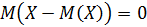
Дисперсия характеризует рассеяние случайной величины относительно математического ожидания.

Математическое ожидание квадрата отклонения случайной величины Х от её математического ожидания M(X) называют дисперсией случайной величины Х и обозначают D(X), т.е.

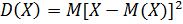
Для дискретных случайных величин эту формулу можно записать в следующем виде:

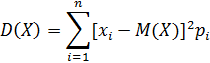
Основные свойства дисперсии:

1.

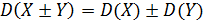
2.

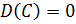
3.

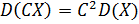
Вопрос 69.

Не нашли, что искали? Воспользуйтесь поиском: