
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Неравенство Чебышева. Лемма: Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию D(Х), то для любого положительного справедливо неравенство:
Лемма: Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию D(Х), то для любого положительного 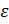 справедливо неравенство:
справедливо неравенство:

Теорема Чебышева.
Теорема Чебышева: При достаточно большом числе независимых случайных величин Х1, Х2, Х3,..., Хn, дисперсия каждой из которых не превышает одного и того же постоянного числа В, для произвольного сколько угодно малого числа 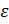 справедливо неравенство
справедливо неравенство
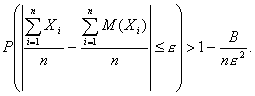
Из теоремы следует, что среднее арифметическое случайных величин при возрастании их числа проявляет свойство устойчивости, т. е. стремится по вероятности к неслучайной величине, которой является среднее арифметическое математических ожиданий этих величин, т.е. вероятность отклонения по абсолютной величине среднего арифметического случайных величин от среднего арифметического их математических ожиданий меньше чем на 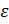 при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием.
при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием.
Вопрос 71
Ранжированием опытных данных называется:
Операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания.
Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.
Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов 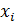 с соответствующими им частотами или частностями.
с соответствующими им частотами или частностями.
Выборочная (или эмпирическая) функция распределения – это неубывающая функция FI (x), которая равна нулю при x <  и равна 1 при x ≥
и равна 1 при x ≥  . Между этими двумя точками функция FI (x) ступенчато возрастает на величину 1/ I каждый раз при переходе через следующую точку x (i) –
. Между этими двумя точками функция FI (x) ступенчато возрастает на величину 1/ I каждый раз при переходе через следующую точку x (i) –
 .
.
Выборочная функция распределения имеет важное теоретическое значение, т.к. при увеличении объема выборки I эмпирическая функция сходится к истинной функции распределения. Однако в практических приложениях чаще используется гистограмма.
Не нашли, что искали? Воспользуйтесь поиском: