
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей - это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой. Например,  – несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу, т.е. D (5, 17) = 1.
– несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу, т.е. D (5, 17) = 1.
Приведение дробей к общему знаменателю - это замена данных дробей равными им дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробей  и
и  является общее кратное чисел п и q, а наименьшим общим знаменателем – их наименьшее кратное К (п, q).
является общее кратное чисел п и q, а наименьшим общим знаменателем – их наименьшее кратное К (п, q).
Задача. Привести к наименьшему общему знаменателю дроби  и
и 
Решение. Разложим числа 15 и 35 на простые множители:
15 = 3×5, 35 = 5×7. Тогда К (15, 35) = 3×5×7 = 105. Поскольку 105 = 15×7 = 35×3, то  =
= 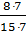 =
= 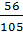 ,
,  =
=  =
=  .
.
Упражнения
1. Известно, что длина отрезка х при единичном отрезке е выражается дробью  . Как могла получиться такая дробь при измерении длины отрезка х? Существуют ли другие дроби, выражающие длину отрезка х при том же единичном отрезке е?
. Как могла получиться такая дробь при измерении длины отрезка х? Существуют ли другие дроби, выражающие длину отрезка х при том же единичном отрезке е?
2. Выберите единицу длины и постройте отрезок, длина которого выражается дробью: а)  ; б)
; б) 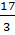 ; в)
; в)  .
.
3. Как установить, равны ли дроби:
а)  и
и 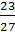 ; б)
; б)  и
и  ?
?
4. На множестве дробей  задано отношение равенства. Постройте граф этого отношения. Каковы особенности этого графа? С чем они связаны?
задано отношение равенства. Постройте граф этого отношения. Каковы особенности этого графа? С чем они связаны?
5. Приведите дроби к наименьшему общему знаменателю.
а)  и
и 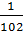 ; б)
; б) 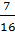 и
и  ; в)
; в) 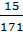 и
и 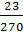
6. Найдите несократимую дробь, равную следующей:
а)  б)
б)  в)
в) 
г)  д)
д) 
Не нашли, что искали? Воспользуйтесь поиском: