Множество положительных рациональных чисел как расширение множества натуральных чисел

Чтобы множество Q+ положительных рациональных чисел являлось расширением множества N натуральных чисел, необходимо выполнение ряда условий.

Первое условие - это существование между N и Q+ отношения включения. Докажем, что N Ì Q+.

Пусть длина отрезка х при единичном отрезке е выражается начальным числом т. Разобьем единичный отрезок на п равных частей. Тогда n -ая часть единичного отрезка будет укладываться в отрезке x точно т × п раз, т.е. длина отрезка х будет выражена дробью . Значит, длина отрезка х выражается и натуральным числом т, и положительным рациональным числом . Но это должно п быть одно и то же число. Поэтому целесообразно считать, что дроби вида являются записями натурального числа т.

Следовательно, N Ì Q+.

Так, например, натуральное число 6 можно представить в виде следующих дробей: , , , , , 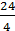и т. д.

Отношение между множествами N и Q+ представлено на рисунке 129.

Числа, которые дополняют множество натуральных чисел до множества положительных рациональных, называются дробными.

Второе условие, которое должно быть выполнено при расширении множества натуральных чисел, - это согласованность операций, т.е. результаты арифметических действий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но выполненных по правилам, сформулированным для положительных рациональных чисел. Нетрудно убедиться в том, что и это условие выполняется.

Пусть а и b - натуральные числа, а + b - их сумма, полученная по правилам сложения в N. Вычислим сумму чисел а и b по правилу сложения в Q+. Так как а = , b = ,то а+b = + = = а+b.

Убедиться в том, что второе условие выполняется и для других операций, можно аналогично.

Третье условие, которое должно быть выполнено при расшире­нии множества натуральных чисел - это выполнимость в Q+ опера­ции, не всегда осуществимой в N. И это условие соблюдено: деление, которое не всегда выполняется в множестве N, в множестве Q+ выполняется всегда.

Сделаем еще несколько дополнений, раскрывающих взаимосвязи между натуральными и положительными рациональными числами.

1. Черту в записи дроби можно рассматривать как знак деления.

Действительно, возьмем два натуральных числа т и п и найдем их
частное по правилу (4) деления положительных рациональных чисел:

т:п = : = = .

Обратно, если дана дробь , то ее можно рассматривать как частное натуральных чисел т и п: = = : = т: п.

2. Любую неправильную дробь можно представить либо в виде натурального числа, либо в виде смешанной дроби.

Пусть – неправильная дробь. Тогда т > п. Если т кратно n, то в этом случае дробь является записью натурального числа. Если число т не кратно п, то разделим т на п с остатком: т = пq + r, где r < п.

Подставим nq + r вместо т в запись и применим правило (1) сложения положительных рациональных чисел:

= = + = q +

Так как r < п, то дробь – правильная. Следовательно, неправильная дробь оказалась представленной в виде суммы натурального числа q и правильной дроби . Это действие называется выделением целой части из неправильной дроби. Например,

= = + = 3+

Сумму натурального числа и правильной дроби принято записывать без знака сложения: т.е. вместо 3 + пишут 3 и называют такую запись смешанной дробью.

Справедливо также утверждение: всякую смешанную дробь можно записать в виде неправильной дроби. Например:

3 = 3 + ₌ + 2 = =

Упражнения

1. Какие из данных чисел являются дробными:

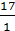а) ; б) ; в) ; г) ?

2. Докажите, что вычитание, умножение и деление натуральных чисел в множестве N и Q+ согласованно.

3. Число 2 умножили на правильную дробь. Какое число получилось – больше или меньше числа 2? А если 2 умножить на неправильную дробь?

4. Может ли при умножении числа 3 на правильную дробь получиться число:

а) меньше 1; б) больше 1?

5. Решите арифметическим методом задачи.

а) В трех гаражах помещается 460 машин. Число машин в первом гараже составляет числа машин, помещающихся во втором, а в третьем гараже в 1 раза больше машин, чем в первом. Сколько машин в каждом гараже?

б) Из двух пунктов, расстояние между которыми 25 км, вышли одновременно навстречу друг другу два пешехода. Один из них проходил в час на км больше другого. С какой скоростью шел каждый, если через 2 ч после выхода расстояние между ними стало 7 км?

Не нашли, что искали? Воспользуйтесь поиском: