Возникновение геометрии

Геометрия зародилась в Древнем Египте как набор правил решения практических задач, возникавших в строительстве, при распределении земельных участков, измерении площадей, объемов и других величин. Свидетельством этому являются египетские пирамиды, построенные около 4800 лет назад, их строительство требовало достаточно сложных и точных геометрических расчетов. Но особенно важной была задача распределения земельных наделов. Этим занимались специальные люди - землемеры, которых греки называли гарпедонаптами, т.е. натягивателями веревок, так как при распределении земли использовались веревки. Но чтобы знать, где и как их натягивать надо было иметь план полей. Так практическая задача распределения участков земли привела к возникновению науки о землемерии.

Обширные сведения о свойствах фигур, накопленные египтянами были заимствованы греками. Произошло это в УП-У вв. до н.э. А так как особенно важной задачей было землемерие, то греки назвали науку о фигурах геометрией, так как с греческого «геос» - земля, а «метрио» -измеряю.

К сказанному можно добавить, что многие геометрические понятия возникли в результате многократных наблюдений реальных предметов той или иной формы, т.е. познавая окружающий мир, люди знакомились и с простейшими геометрическими формами. Овладению этим знанием способствовало изготовление орудий, имеющих сравнительно правильную геометрическую форму, строительство жилья, шитье одежды, изготовление посуды, украшений.

Огромное влияние на развитие геометрических представлений оказали систематические астрономические наблюдения. Они способствовали возникновению понятий шара, окружности, угла, угловой меры.

Развитие землемерия, обобщение накопленного опыта наблюдений привело к созданию практических правил измерения земельных участков, нахождения площадей и объемов простейших фигур, правил, необходимых для строительства, и др. Так, формулы для вычисления площадей земельных участков, имеющих форму треугольника, трапеции, встречаются у древних египтян, вавилонян. К ХУН-ХУ1 вв. до н.э. были установлены такие ее факты, как теорема Пифагора, найдено выражение для подсчета объема шара и многие другие. Но выступали они не как логически доказанные утверждения, а как выводы из опыта.

Таким образом, геометрия возникла как прикладная наука, как собрание правил, необходимых для решения практических задач: сравнения фигур, нахождения геометрических величин, простейших геометрических построений.

Практические правила постепенно приводились в систему. Кроме того, одни правила стали выводиться из других и обосновываться посредством рассуждений. Возникло доказательство, правила стали превращаться в теоремы, которые доказывались без прямых ссылок на опыт. Вообще совершенствование геометрических знаний шло по пути их отделения от опыта - в результате предметом геометрии стали не реальные, а идеальные фигуры, т.е. фигуры, являющиеся образами предметов, в которых абстрагируются от всего, кроме формы. Более того, эти фигуры стали дополняться свойствами, которыми реальные предметы не обладают. Например, понятие прямой, возникшее как отражение такого свойства реальных предметов, как протяженность, было дополнено представлением о ее бесконечности.

Получение новых геометрических утверждений при помощи растлений относится к VI в. до н.э. и связано с именем древнегреческого математика Фалеса. Считают, что им доказаны свойства равнобедренного треугольника, равенство вертикальных углов и ряд других фактов.

К III в. до н.э. геометрия становится дедуктивной наукой, одновременно решая многие практические задачи: дает точно обоснованные правила для построения фигур с заданными свойствами, позволяет различными способами сравнивать фигуры, по одним свойствам фигуры делать выводы о других ее свойствах и т.д.

Основные достижения в области математики были систематизированы около 300 лет до н.э. греческим ученым Евклидом и изложены в его знаменитом труде «Начала», состоящем из тринадцати книг. Это сочинение является первым дошедшим до нас строгим логическим построением геометрии.

Каждая книга «Начал» начинается с определений основных понятий. Так, в книге по геометрии 35 определений. Среди них определения точки, линии, прямой, поверхности.

Точка есть то, что не имеет частей.

Линия есть длина без ширины.

Прямая линия есть та, которая одинаково лежит относительно всех своих точек.

Поверхность есть то, что имеет длину и ширину.

Кроме перечисленных даются определения плоского и прямого углов, перпендикуляра, тупого и острого углов, круга, окружности, треугольника и его видов, четырехугольника и его видов и др. Завершает этот список определение параллельных прямых: «Параллельные прямые суть те, которые лежат в одной плоскости и, будучи продолженными в обе стороны, нигде не встречаются».

За определениями следует пять постулатов следующего содержания. Требуется, чтобы:

1) от каждой точки до каждой другой можно было провести прямую;

2) ограниченную прямую можно было продолжить неопределенно;

3) из любого центра можно было описать окружность любым радиусом;

4) все прямые углы были равны;

5) если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны.

Затем формулировались аксиомы:

1) равные одному и тому же третьему также равны и между собой;

2) если к равным прибавить равные, то целые будут равны;

3)если от равных отнять равные, то полученные остатки буду-равны;

4)совмещающиеся друг с другом равны;

5)целое больше своей части.

Видим, что начальные определения евклидовой геометрии - это описания ее основных объектов: точки, прямой, плоскости, угла и т.д. Постулаты выражают возможность основных построений. При этом прямая мыслится как непрерывная, неограниченно делимая, но не состоящая из точек, что соответствует наглядному представлению – прямую проводят по линейке, а не строят по точкам. Аксиомы, сформулированные Евклидом, относятся к величинам: длине отрезка, величине угла, площади фигуры. У Евклида «равные» понимались как «равновеликие».

За постулатами и аксиомами, которые рассматривались как утверждения, принимаемые без доказательств, формулировались теоремы и задачи на построение. Они располагались в строгой последовательности так, что каждое последующее опирается на предыдущее, а также на постулаты и аксиомы.

Определения, постулаты, аксиомы и дальнейшие выводы в геометрии Евклида имели наглядный, опирающийся на практику смысл, хотя выражали его в идеализированном, абстрактном виде.

Таким образом, геометрия сложилась как наука о пространственных формах и отношениях, рассматриваемых отвлеченно от их математического содержания. В Древней Греции она сформировалась в абстрактную логическую систему, в основе которой лежат первоначальные понятия и аксиомы, новые факты формулируются в виде теорем и выводятся дедуктивным способом, а каждое новое понятие вводится с помощью определения на основе ранее введенных понятий.

«Начала» Евклида оставили глубокий след в истории и в течение многих веков служили образцом научного изложения математики.

Упражнения

1. Площадь круга египтяне считали равной площади квадрата, сторона которого составляет диаметра. Чему при таких подсчетах оказывается равным число ?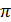

2. Древнегреческий математик Фалес доказал, что если в прямоугольном треугольнике АВС гипотенузу АС разделить точкой О пополам, то АО = ВО. Можете ли вы доказать это утверждение?

3. Узнав, что стороны треугольника равны 3, 4 и 5, ученик, с сдавшись на теорему Пифагора, сделал заключение, что данный треугольник прямоугольный. Обоснованно ли его заключение?

4. В каждой нижеприведенной теореме выделите условие и заключение:

а) хорда, не проходящая через центр окружности, меньше диаметра этой окружности;

б) углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые;

в) для того чтобы два угла в сумме составляли 180°, достаточно, чтобы они были смежными.

5. Опровергните следующие утверждения:

а) если диагонали четырехугольника перпендикулярны между собой, то данный четырехугольник есть ромб;

б) если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого, то такие треугольники равны между собой.

6. Для каждой из приведенных ниже теорем сформулируйте обратное утверждение и установите, истинно ли оно:

а) сумма смежных углов равна 180°;

б) соответственные углы, получающиеся при пересечении двух параллельных прямых третьей, равны;

в) если в треугольнике один угол тупой или прямой, то два других острые.

Не нашли, что искали? Воспользуйтесь поиском: