
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Положительные рациональные числа
Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нем классы эквивалентности. В каждом таком классе содержатся равные между собой дроби. Например, множество дробей  – это один класс, множество дробей
– это один класс, множество дробей 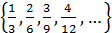 – это другой класс и т. д.
– это другой класс и т. д.
Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби - это различные записи одного и того же положительного рационального числа.
 Определение. Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Определение. Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, о дроби  мы должны говорить, что она является записью некоторого рационального числа. Однако часто для краткости
мы должны говорить, что она является записью некоторого рационального числа. Однако часто для краткости
говорят:  это рациональное число.
это рациональное число.
Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на этом множестве отношение равенства.
 Определение. Если положительное рациональное число а представлено дробью
Определение. Если положительное рациональное число а представлено дробью  , а положительное рациональное число b – другой дробью
, а положительное рациональное число b – другой дробью  , то а=b тогда и только тогда, когда тq = пр.
, то а=b тогда и только тогда, когда тq = пр.
Из данного определения следует, что равные рациональные числа представляются равными дробями. Среди всех записей любого положительного рационального числа выделяют дробь, которая является несократимой, и доказывают, что любое рациональное число представимо единственным образом несократимой дробью (мы это доказательство опускаем). Для того чтобы рациональное число  представить несократимой дробью, достаточно числитель т и знаменатель разделить на их наибольший общий делитель.
представить несократимой дробью, достаточно числитель т и знаменатель разделить на их наибольший общий делитель.
Выясним теперь, как определяются арифметические действия с положительными рациональными числами.
Пусть при некотором единичном отрезке е длина отрезка х выражается дробью  , а длина отрезка у – дробью
, а длина отрезка у – дробью  , и пусть отрезок z состоит из отрезков х и у. Тогда n -ая часть отрезка е укладывается в отрезке z т+р раз, т.е. длина отрезка z выражается дробью
, и пусть отрезок z состоит из отрезков х и у. Тогда n -ая часть отрезка е укладывается в отрезке z т+р раз, т.е. длина отрезка z выражается дробью 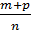 .
.
Поэтому полагают, что  .
.
 Определение. Если положительное рациональное число а представлено дробью
Определение. Если положительное рациональное число а представлено дробью  а положительное рациональное число b – дробью
а положительное рациональное число b – дробью  ,
,
то их суммой называется число а + b, которое представляется дробью 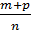 .
.
Таким образом, по определению

Можно доказать, что при замене дробей  и
и  , представляющих числа а и b, равными им дробями, дробь
, представляющих числа а и b, равными им дробями, дробь 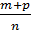 заменяется равной ей дробью. Поэтому сумма рациональных чисел не зависит от выбора представляющих их дробей.
заменяется равной ей дробью. Поэтому сумма рациональных чисел не зависит от выбора представляющих их дробей.
В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применять правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
(" а,b ÎQ+) а + b = b + а;
(" а, b, с ÎQ+) (а + b) + с = а + (b + с).
Докажем, например, коммутативность сложения. Представим числа а и b дробями  и
и  . Тогда сумма а + b представляется дробью
. Тогда сумма а + b представляется дробью 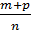 , а сумма b + а- дробью
, а сумма b + а- дробью  . Так как т, р, п- натуральные числа, то т + р = р + т и, следовательно, а + b = b + а. Таким образом, коммутативность сложения положительных рациональных чисел вытекает из коммутативности сложения натуральных чисел.
. Так как т, р, п- натуральные числа, то т + р = р + т и, следовательно, а + b = b + а. Таким образом, коммутативность сложения положительных рациональных чисел вытекает из коммутативности сложения натуральных чисел.
Прежде чем сформулировать определение умножения положительных рациональных чисел, рассмотрим следующую задачу: известно, что длина отрезка X выражается дробью  при единице длины Е, а длина единичного отрезка измерена при помощи единицы Е1 и выражается дробью
при единице длины Е, а длина единичного отрезка измерена при помощи единицы Е1 и выражается дробью  . Как найти число, которым будет представлена длина отрезка X, если измерить ее при помощи единицы длины Е1?
. Как найти число, которым будет представлена длина отрезка X, если измерить ее при помощи единицы длины Е1?
Так как X =  Е, то п X = т×Е, а из того, что Е =
Е, то п X = т×Е, а из того, что Е =  × Е1 следует, что q × Е = р×Е1. Умножим первое полученное равенство на q, а второе на т. Тогда (п q)× X = (тq) × Е и (т q) ×Е = (тр) ×Е1, откуда (п q)Х = (тр)×Е1. Это равенство показывает, что длина отрезка x при единице длины Е выражается дробью
× Е1 следует, что q × Е = р×Е1. Умножим первое полученное равенство на q, а второе на т. Тогда (п q)× X = (тq) × Е и (т q) ×Е = (тр) ×Е1, откуда (п q)Х = (тр)×Е1. Это равенство показывает, что длина отрезка x при единице длины Е выражается дробью  , а значит,
, а значит,  , т.е. умножение дробей связано с переходом от одной единицы длины к другой при измерении длины одного и того же отрезка.
, т.е. умножение дробей связано с переходом от одной единицы длины к другой при измерении длины одного и того же отрезка.
 Определение. Если положительное число а представлено дробью
Определение. Если положительное число а представлено дробью  , а положительное рациональное число и – дробью
, а положительное рациональное число и – дробью  , то их произведением называется число аb, которое представляется дробью
, то их произведением называется число аb, которое представляется дробью  .
.
Таким образом, по определению,
 (2)
(2)
Можно доказать, что при замене дробей  и
и  , представляющих числа а и b, равными им дробями, дробь
, представляющих числа а и b, равными им дробями, дробь  заменяется равной ей дробью. Поэтому произведение чисел а и b не зависит от выбора представляющих их дробей.
заменяется равной ей дробью. Поэтому произведение чисел а и b не зависит от выбора представляющих их дробей.
Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания. Доказательство этих свойств основывается на определении умножения и сложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел. Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множестве Q+.
 Определение. Пусть а и b - положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а = b + с.
Определение. Пусть а и b - положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а = b + с.
В этом же случае считают, что число а больше числа b. Пишут b < а, а>b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа а и b представлены дробями  и
и  (т.е. дробями, имеющими одинаковые знаменатели), то а < b в том и только в том случае, когда т <р.
(т.е. дробями, имеющими одинаковые знаменатели), то а < b в том и только в том случае, когда т <р.
3. Если рациональные числа а и b представлены дробями  и
и  (т.е. дробями, имеющими разные знаменатели), то а < b в том и только в том случае, когда тq < пр.
(т.е. дробями, имеющими разные знаменатели), то а < b в том и только в том случае, когда тq < пр.
4. В множестве положительных рациональных чисел нет наименьшего числа.
5. Между любыми двумя различными числами а и b из Q+ заключено бесконечно много чисел этого же множества. Это свойство называют свойством плотности множества +.
6. В множестве положительных рациональных чисел нет наибольшего числа.
Вычитание положительных рациональных чисел определяется как операция, обратная сложению, т.е. это такая операция, которая удовлетворяет условию: а-b = с тогда и только тогда, когда а = b + с.
Разность а-b положительных рациональных чисел существует тогда и только тогда, когда b < а. Если разность а-b существует, то она единственна.
Используя определение и условие существования разности, можно получить правило вычитания положительных рациональных чисел, представленных дробями  и
и  , где т<р:
, где т<р:
 (3)
(3)
Деление положительных рациональных чисел определяется как операция, обратная умножению, т.е. это такая операция, которая удовлетворяет условию: а: b = с тогда и только тогда, когда а = bс.
Из этого определения и правила нахождения произведения положительных рациональных чисел можно получить правило деления положительных рациональных чисел, представленных дробями 
 (4)
(4)
Из этого правила следует, что частное положительных рациональныхчисел всегда существует.
Упражнения
1. Рациональное число представлено дробью 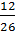 . Может ли оно быть представлено дробью
. Может ли оно быть представлено дробью  ? А дробью
? А дробью  ?
?
2. Какие из следующих дробей несократимые:
а)  ; ------ б)
; ------ б)  ; в)
; в)  ?
?
3. Докажите свойство ассоциативности сложения положительных рациональных чисел. Какие преобразования выражений можно выполнять на его основе?
4. Вычислите значения следующих выражений, записав их в виде несократимых дробей; выполненные преобразования обоснуйте.
а)  ; в)
; в) 
5. Запишите законы умножения положительных рациональных чисел и докажите их. Какие преобразования выражений можно выполнять на их основе?
6. Вычислите значения следующих выражений, записав их в виде несократимых дробей; выполненные преобразования обоснуйте.
а)  ;------------- б)
;------------- б)  ×
× 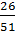 в)
в) 
7. Докажите, что отношение «меньше» на множестве Q+ является отношением порядка.
8. «Сравните числа:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
9. Найдите три дроби, которые заключены между дробями  и
и  .
.
10. Найдите значения следующих выражении:
а)  ; б)
; б)  ; в)
; в) 
11. Решите задачи арифметическим способом.
а) Прямоугольник разделили на 8 равных частей. Сначала закрасили  прямоугольника, потом
прямоугольника, потом  , затем
, затем  . Весь ли прямоугольник закрасили?
. Весь ли прямоугольник закрасили?
б) Мальчик отпил  чашки черного кофе и долил молока, затем отпил
чашки черного кофе и долил молока, затем отпил  чашки и опять долил молока, потом отпил еще
чашки и опять долил молока, потом отпил еще  чашки и снова долил молока. Наконец, он допил кофе с молоком. Чего больше выпил мальчик - кофе или молока?
чашки и снова долил молока. Наконец, он допил кофе с молоком. Чего больше выпил мальчик - кофе или молока?
в) Двум машинисткам было поручено перепечатать рукопись. Первая машинистка перепечатала  всей рукописи, а вторая –
всей рукописи, а вторая –  всей рукописи. Сколько страниц в рукописи, если первая машинистка перепечатала на 7 страниц больше, чем вторая?
всей рукописи. Сколько страниц в рукописи, если первая машинистка перепечатала на 7 страниц больше, чем вторая?
г) В первом вагоне в 1  раза больше груза, чем во втором. Если из первого вагона выгрузить 5
раза больше груза, чем во втором. Если из первого вагона выгрузить 5  т, а во второй добавить 14
т, а во второй добавить 14  т, то груза в вагонах будет поровну. Сколько тонн груза в каждом вагоне?
т, то груза в вагонах будет поровну. Сколько тонн груза в каждом вагоне?
Не нашли, что искали? Воспользуйтесь поиском: