
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Параллельные и перпендикулярные прямые
 Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.
Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.
Если прямая а параллельная прямой b, то пишут а || b.
Рассмотрим некоторые свойства параллельных прямых, и прежде всего признаки параллельности.
Признаками называют теоремы, в которых устанавливается наличие какого-либо свойства объекта, находящегося в определенной ситуации. В частности, необходимость рассмотрения признаков параллельности прямых вызвана тем, что нередко в практике требуется решить вопрос о взаимном расположении двух прямых, но в то же время нельзя непосредственно воспользоваться определением.
Рассмотрим следующие признаки параллельности прямых:
1. Две прямые, параллельные третьей, параллельны друг другу.
2. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Справедливо утверждение, обратное второму признаку параллельности прямых: если две параллельные прямые пересечены третьей, то внутренние накрест лежащие углы равны, а сумма односторонних углов равна 180°.
Важное свойство параллельных прямых раскрывается в теореме, носящей имя древнегреческого математика Фалеса: если параллельные прямые, пересекающие стороны угла отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
 Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Если прямая а перпендикулярна прямой b, то пишут а ^ b.
Основные свойства перпендикулярных прямых нашли отражение в двух теоремах:
1. Через каждую точку прямой можно провести перпендикулярную к ней прямую, и только одну.
2. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий концом их точку пересечения. Конец этого отрезка называется основанием перпендикуляра.
Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.
Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой.
Упражнения
1. Какие свойства параллельных прямых включены в их определение и в аксиому параллельных?
2. Как построить параллельные прямые с помощью линейки и чертежного треугольника? На каком признаке параллельности основано это построение?
3. Верны ли следующие утверждения:
а) Если две прямые пересечены третьей, то соответственные углы равны.
б) Если при пересечении двух параллельных прямых третьей накрест лежащие углы равны, то эти две прямые параллельны.
4. Внесите изменения в утверждения, данные в задании 3, чтобы они стали верными.
5. Как практически проверить, параллельны ли две данные прямые, начерченные на бумаге?
6. Укажите не менее трех свойств перпендикулярных прямых. Какое из них включено в определение? Какие свойства должны быть доказаны быть доказаны?
7. Докажите, что две прямые, лежащие в одной плоскости и перпендикулярные к одной и той же третьей прямой, параллельны между собой.
8. Углы АВС и СВD - смежные, угол СВD равен  d. Определите угол между перпендикуляром, проведенным из точки В к прямой АD, и биссектрисой угла AВС.
d. Определите угол между перпендикуляром, проведенным из точки В к прямой АD, и биссектрисой угла AВС.
Треугольники
Треугольник - одна из простейших геометрических фигур. Но его изучение породило целую науку - тригонометрию, которая возникла из практических потребностей при измерении земельных участков, составлении карт местности, конструировании различных механизмов.
Первые упоминания о треугольнике и его свойствах содержатся в египетских папирусах. Например, в них предлагается находить площадь равнобедренного треугольника как произведение половины основания на боковую сторону, хотя для любого равнобедренного треугольника с малым углом при вершине, противоположной основанию, такой способ дает приближенное значение площади.
Многие свойства треугольников были открыты и доказаны математиками Древней Греции. Среди них - знаменитая теорема Пифагора.
Рассмотрим основные понятия, связанные с треугольником.
Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.
Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником (или плоским треугольником).
В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии.
Углом треугольника AВС при вершине А называется угол, образованный полупрямыми АВ и АС.
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающими более быстрое решение вопроса об отношениях между ними. Таких признаков три.
1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.
Равнобедренные треугольники обладают рядом свойств, например:
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Отметим еще несколько важных свойств треугольников.
1. Сумма углов треугольника равна 180°.
Из этого свойства следует, что в любом треугольнике хотя бы два угла острые.
2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
3. В любом треугольнике каждая сторона меньше суммы двух других сторон.
Для прямоугольного треугольника с углом 30° справедливо следующее свойство: катет, противолежащий этому углу, равен половине гипотенузы.
Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Упражнения
1. Можно ли из палочек длиной 10 см, 6 см, 4 см сложить треугольник?
2. Как установить, равны два треугольника или нет?
3. Назовите свойства равнобедренного треугольника. Какие из них содержатся в определении, а какие надо доказывать?
4. Отвечают ли требованиям, предъявляемым к определениям понятий, следующие формулировки:
а) Треугольник, у которого две стороны и два угла равны, называется равнобедренным.
б) Средней линией треугольника называется прямая, проходящая через середины двух его сторон.
в) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон и параллельный основанию.
5. Могут ли равносторонние треугольники быть: а) прямоугольными; б) тупоугольными? Ответ обоснуйте.
6. Установите вид треугольника (по углам), если один из его внутренних углов: а) равен сумме двух других; б) больше суммы двух других; в) меньше суммы двух других.
7. Можно ли какой-нибудь треугольник разрезать на два остроугольных?
8. Прямая р пересекает отрезок АВ в точке О, являющейся его серединой. Докажите, что точки А и В находятся на одинаковом расстоянии от прямой р.
9. Отрезки АВ и СD пересекаются в точке О, являющейся серединой каждого. Докажите, что АС и BD параллельны.
10. Столяру нужно заделать отверстие треугольной формы. Какие он должен снять размеры, чтобы изготовить латку? Что он должен измерить, если отверстие имеет форму: а) прямоугольного треугольника; б) равностороннего треугольника?
Четырехугольники
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки - его сторонами.
Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называют четырехугольником (или плоским четырехугольником).
Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.
 Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВСD (рис. 138) вершины А и В - соседние, а вершины А и С- противолежащие-стороны АВ и ВС - соседние, ВС и АD – противолежащие; отрезки АС и ВD диагонали данного четырехугольника.
Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВСD (рис. 138) вершины А и В - соседние, а вершины А и С- противолежащие-стороны АВ и ВС - соседние, ВС и АD – противолежащие; отрезки АС и ВD диагонали данного четырехугольника.
Четырехугольники бывают выпуклые и невыпуклые. Так, четырехугольник АВСD (рис. 138) - выпуклый, а четырехугольник КРМТ (рис. 139) невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.
Параллелограммом называется четырехугольник, у которого противолежащие стороны параллельны.
Пусть АВСD - параллелограмм. Из вершины В на прямую АD опустим перпендикуляр ВЕ. Тогда отрезок ВЕ называется высотой параллелограмма, соответствующей сторонам ВС и АD (рис. 140). Отрезок СМ - высота параллелограмма АВСD, соответствующая сторонам СD и АВ.
Чтобы упростить распознавание параллелограммов, рассматривают следующий признак: если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то данный четырехугольник - параллелограмм.
Ряд свойств параллелограмма, которые не содержатся в его определении, формулируют в виде теорем и доказывают. Среди них:
1. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
2. У параллелограмма противолежащие стороны и противолежащие углы раны.
Рассмотрим теперь определение трапеции и ее основное свойство.
Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны.
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции обладает следующим свойством: она параллельна основаниям и равна их полусумме.
Из множества параллелограммов выделяют прямоугольники и ромбы.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Исходя из этого определения, можно доказать, что диагонали прямоугольника равны.
Ромбом называется параллелограмм, у которого все стороны равны.
Пользуясь этим определением, можно доказать, что диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Из множества прямоугольников выделяют квадраты.
Квадратом называется прямоугольник, у которого все стороны равны.
Так как стороны квадрата равны, то он является также ромбом. Следовательно, квадрат обладает свойствами прямоугольника и ромба.
Упражнения
1. Назовите пять свойств параллелограмма. Какие из них содержатся в его определении, а какие надо доказывать?
2. Может ли диагональ параллелограмма равняться его стороне?
3. Постройте параллелограмм АВСD и его высоты, выходящие из вершины С.
4. Обоснуйте следующий способ построения параллелограмма, предложенный младшим школьникам: «Проведи две пересекающиеся прямые. При помощи циркуля отложи на одной прямой от точки пересечения равные отрезки. Затем на другой прямой таким же образом отложи равные отрезки (не обязательно такой же длины, что и на первой прямой). Получится параллелограмм».
5. Назовите пять свойств прямоугольника. Какие из них содержатся в его определении, а какие надо доказывать? Докажите, что диагонали в прямоугольнике равны.
6. Докажите, что всякий параллелограмм, у которого диагонали равны, есть прямоугольник.
7. Мастерская изготовила пластины четырехугольной формы. Как проверить, будет ли пластина иметь форму прямоугольника, располагая лишь линейкой с делениями.
8. Мастеру надо изготовить щит, который должен полностью закрыть нишу прямоугольной формы. Какие он должен снять размеры, чтобы изготовить этот щит?
9. Докажите, что параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.
10. Докажите, что почтовый конверт склеивается из листа бумаги имеющей форму ромба (припуски на склеивание не учитывать).
11. Паркетчик, проверяя, имеет ли выпиленный четырехугольник форму квадрата, убеждается, что диагонали равны и пересекаются под прямым углом. Достаточна ли такая проверка?
12. Столяру нужно изготовить подставку в форме четырехугольника. Какие размеры должен он иметь для выполнения заказа? Что должен измерить столяр, если подставка имеет форму: а) параллелограмма; б) прямоугольника; в) ромба; г) квадрата?
13. 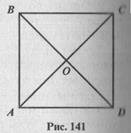 Из приведенных ниже восьми свойств фигуры (рис. 141) выделите минимальное число таких, из которых следовали бы все остальные Выделив исходные, докажите все остальные:
Из приведенных ниже восьми свойств фигуры (рис. 141) выделите минимальное число таких, из которых следовали бы все остальные Выделив исходные, докажите все остальные:
1) АВСD - прямоугольник;
2) АВ = ВС;
3) АС ^ ВО;
4) 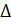 АОВ =
АОВ = 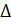 ВОС =
ВОС = 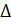 СОD =
СОD = 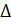 DОА;
DОА;
5) АС = ВD;
6) О- центр симметрии;
7) АВ = СD;
8) 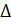 АВС =
АВС = 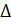 АDС.
АDС.
14. Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме.
15. Докажите, что отрезки прямых, соединяющих середины смежных сторон равнобедренной трапеции, образуют ромб.
16. Земельный участок, имеющий форму трапеции, отдан под спортивный городок. Какие размеры должен снять землемер, чтобы начертить план этого участка?
Многоугольники
Обобщением понятия треугольника и четырехугольника является понятие многоугольника. Определяется оно через понятие ломаной.
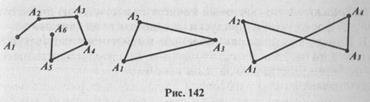
Ломаной А,А2А3... Аn называется фигура, которая состоит из точек А1, А2, А3,..., Аn и соединяющих их отрезков А1А2, А2А3,..., Аn-1,Аn. Точки А1, А2, А3,..., Аn называются вершинами ломаной, а отрезки А1А2,А2А3,..., Аn-1Ап - ее звеньями.
Если ломаная не имеет самопересечений, то она называется простой. Если ее концы совпадают, то она называется замкнутой. О ломаных, изображенных на рисунке 142, можно сказать, что: А1А2А3А4А5А6 - простая; А1А2А3 - простая замкнутая; А1А2А3А4 - замкнутая ломаная, но она не является простой, так как имеет самопересечение.
Длиной ломаной называется сумма длин ее звеньев.
|
Известно, что длина ломаной не меньше длины отрезка, соединяющего ее концы.
Многоугольником называется простая замкнутая ломаная, если ее соседние звенья не лежат на одной прямой.
Вершины ломаной называются вершинами многоугольника, а ее звенья - его сторонами. Отрезки, соединяющие несоседние вершины, называются диагоналями.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая - внешней областью многоугольника (или плоским многоугольником).
Различают выпуклые и невыпуклые многоугольники.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Правильным является равносторонний треугольник, правильным четырехугольником - квадрат.
Углом выпуклого многоугольника при данной вершине называется угол, образуемый его сторонами, сходящимися в этой вершине.
Известно, что сумма углов выпуклого n -угольника равна 180°×(n - 2).
В геометрии, кроме выпуклых и невыпуклых многоугольников, рассматривают еще многоугольные фигуры.
Многоугольной фигурой называется объединение конечного множества многоугольников (рис.143).
|
Многоугольники, из которых состоит многоугольная фигура, могут не иметь общих внутренних точек (рис. 143, а, в); могут иметь общие внутренние точки (рис. 143,б).
Говорят, что многоугольная фигура F состоит из многоугольных фигур, если она является их объединением, а сами фигуры не имеют общих внутренних точек. Например, о многоугольных фигурах, изображенных на рисунке 143,а,в, можно сказать, что они состоят из двух многоугольных фигур или что они разбиты (каждая) на две многоугольные фигуры.
Упражнения
1. Сформулируйте определение простой замкнутой ломаной и постройте такую фигуру.
2. Расстояние от пункта А до пункта В равно 3 км, а от пункта В до пункта С вдвое больше. Каково наибольшее и наименьшее расстояние от пункта А до пункта С?
3. Могут ли все углы выпуклого четырехугольника быть: а) тупыми; б) острыми; в) прямыми?
4. Сколько прямых углов может иметь: а) параллелограмм; б) трапеция?
5. Дан квадрат, разрезанный по диагонали на два треугольника. Сколько выпуклых многоугольников, отличных от квадрата, можно составить из этих треугольников?
6. Квадрат разрезан по своим диагоналям. Сколько выпуклых многоугольников, отличных от квадрата, можно составить из четырех образовавшихся треугольников?
7. Разрежьте по диагонали произвольный прямоугольник и из полученных треугольников составьте всевозможные выпуклые многоугольники.
8. Назовите свойства правильного многоугольника. Можете ли вы привести пример многоугольника, не являющегося правильным, но имеющего: а) все равные между собой углы; б) все равные стороны?
9. Сколько сторон имеет многоугольник, если сумма его внутренних углов равна 40 d?
10. Можно ли сложить паркет из правильных: а) треугольников, б) пятиугольников; в) восьмиугольников; г) восьмиугольников и квадратов?
Окружность и круг
Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки, называемой центром.
Любой отрезок, соединяющий точку окружности с ее центром, называется радиусом окружности. Радиусом называется также расстояние от любой точки окружности до ее центра.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.
|
Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние -радиусом круга.
Границей круга является окружность с теми же центром и радиусом.
Напомним некоторые свойства окружности и круга.
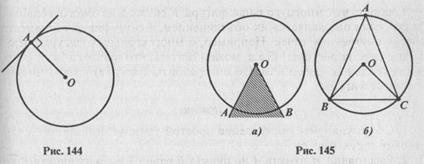
Говорят, что прямая и окружность касаются, если они имеют единственную общую точку. Такую прямую называют касательной, а общую точку прямой и окружности - точкой касания. Доказано, что если прямая касается окружности, то она перпендикулярна радиусу, проведенному в точку касания (рис.144). Справедливо и обратное утверждение.
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу. На рисунке 145,а штриховкой отмечен центральный угол, которому соответствует дуга АВ.
Угол, вершина которого лежит на окружности, а стороны пересекают ее, называется вписанным в эту окружность. Угол ВАС на рисунке 145, б вписан в окружность. Говорят также, что угол А опирается на хорду ВС. Прямая ВС разбивает окружность на две дуги. Центральный угол, соответствующий той дуге, которая не содержит точку А, называется центральным, соответствующим данному вписанному углу.
Угол, вписанный в окружность, обладает следующим свойством: он равен половине соответствующего центрального угла.
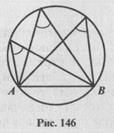 Из этого утверждения следует, что вписанные углы, стороны которых проходят через точки А и В, принадлежащие окружности, а вершины лежат по одну сторону от прямой АВ, равны (рис. 146).
Из этого утверждения следует, что вписанные углы, стороны которых проходят через точки А и В, принадлежащие окружности, а вершины лежат по одну сторону от прямой АВ, равны (рис. 146).
В частности, углы, опирающиеся на диаметр, - прямые.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Чтобы описать окружность около треугольника, надо найти ее центр. Правило его нахождения обосновывается следующей теоремой:
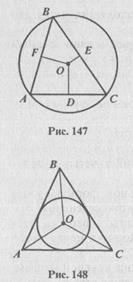 Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к его сторонам, проведенных через середины этих сторон (рис. 147).
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к его сторонам, проведенных через середины этих сторон (рис. 147).
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Правило нахождения центра такой окружности обосновывается следующей теоремой:
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис. 148).
Из последних двух теорем следует, что биссектрисы треугольника пересекаются в центре вписанной окружности, а серединные перпендикуляры - в центре описанной. Можно доказать, что медианы треугольника, так же как и его высоты, пересекаются в одной точке. Точку пересечения медиан называют центром тяжести треугольника, а точку пересечения высот - ортоцентром.
Таким образом, во всяком треугольнике существует четыре точки, их называют замечательными: центр тяжести, центры вписанной и описанной окружностей и ортоцентр, – в которых пересекаются соответствующие элементы этого треугольника – медианы, биссектрисы, серединные перпендикуляры и высоты.
В связи с тем, что во всякий треугольник можно вписать окружность и около всякого треугольника можно описать окружность, возникает вопрос: обладают ли аналогичным свойством четырехугольники? Оказывается, для того чтобы в четырехугольник можно было вписать или около него описать окружность, необходимо, чтобы он был правильным.
Около всякого правильного многоугольника можно описать окружность и во всякий правильный многоугольник можно вписать окружность, причем центры вписанной и описанной окружностей совпадают.
Упражнения
1. Сколько окружностей можно провести через: а) одну точку; б) две точки; в) три точки, не лежащие на одной прямой?
2. Как расположены центры окружностей одного и того же радиуса, проходящих через данную точку?
3. Как расположены центры окружностей, проходящих через две данные точки?
4. Окружность разделена в отношении 1:2:3, и точки деления соединены между собой отрезками. Определите углы полученного треугольника.
5. Докажите, что все углы, опирающиеся на диаметр окружности, прямые.
6. Угол между двумя радиусами равен 150°. Определите угол между касательными, проведенными через концы этих радиусов.
7. Как найти центр окружности, если он неизвестен?
8. В данной окружности проведены два диаметра и концы их попарно соединены хордами. Докажите, что получившийся четырехугольник - прямоугольник.
9. В каком месте открытого участка треугольной формы нужно поместить фонарь, чтобы все три угла были одинаково освещены?
10. В треугольной пластине нужно так просверлить отверстие, чтобы оно было равноудалено от ее сторон. Где находится центр этого отверстия?
11. Стекольщику надо вырезать стекло для окна круглой формы. Как и что он должен измерить, чтобы вырезать нужное стекло, располагая только рулеткой.
12. Острый угол между диагоналями прямоугольника 60°, меньшая его сторона 1,5 дм. Вычислите радиус окружности, описанной около этого прямоугольника.
13. Угол при вершине равнобедренного треугольника 120°, боковая его сторона 4 дм. Вычислите диаметр окружности, описанной около треугольника.
Не нашли, что искали? Воспользуйтесь поиском: