Свойства векторного произведения

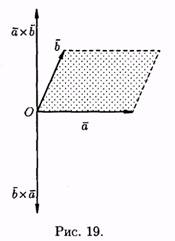
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa) (см. рис. 19).

Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а, b, а хb и a, b, bxaпротивоположной ориентации). Стало быть axb = -(bxa).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l(а хb) = (lа) х b = а х (lb).

Пусть l>0. Вектор l(ахb) перпендикулярен векторам а и b. Вектор (lа)хb также перпендикулярен векторам а и b (векторы а, lа лежат в одной плоскости). Значит, векторыl(ахb) и (lа)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

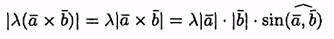
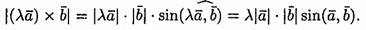
Поэтому l(a хb)= lахb. Аналогично доказывается при l<0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

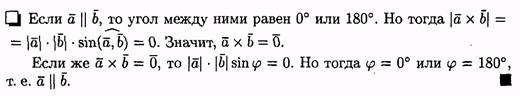
В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

Примем без доказательства.

Не нашли, что искали? Воспользуйтесь поиском: