Смешанное произведение векторов их свойства и применение

Геометрический смысл смешанного произведения: если тройка векторов правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: . В случае левой тройки смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: . Если , и компланарны, то их смешанное произведение равно нулю.

Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах , и равен модулю смешанного произведения этих векторов:

Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения:

1°

2°

3° Три вектора компланарны тогда и только тогда, когда

4° Тройка векторов является правой тогда и только тогда, когда . Если же , то векторы , и образуют левую тройку векторов.

5°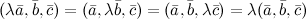

6°

7°

8°

9°

10° Тождество Якоби:

Если векторы , и заданы своими координатами, то их смешанное произведение вычисляется по формуле

ПРИМЕР. Задание. Вычислить объем пирамиды, построенной на векторах , ,

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов , и :

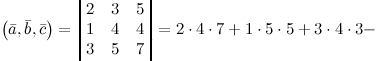
Условия коллинеарности и компланарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Не нашли, что искали? Воспользуйтесь поиском: