Векторы. Линейные операции над ними. Зависимость векторов. Базис. Декартова система координат. Деление отрезка в данном отношении.

Вектором назыв.направленный отрезок опред-ся длиной и направлением в пространстве, бывают векторы несвободные. Скользящие векторы находят наиб-ее распространение, он может быть приложен к любой точке пространства и будет одинаков. Векторы равны (скользящие), если равны их длины и они одинаково направлены. Векторы назыв. коллинеарными, если они расположены на параллельных прямых.

Скалярной величиной или скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, цена, количество проданного товара, стоимость и т.д.

Векторной величиной или вектором называется величина, для задания которой кроме численного значения необходимо указать и ее направление в пространстве, например, изменение темпов производства (рост или падение), колебание курса акций на бирже и т.д.

Векторная величина графически обычно изображается как связанный вектор или направленный отрезок, т.е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление, свободный вектор или просто вектор представляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется: направлением; длиной (модулем).

Линейные операции над векторами

Сложение вектора производится по правилу параллелограмма: векторы и 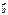сносятся в общую точку 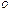(рис. 4.1), на них строят параллелограмм и его диагональ называют суммой векторов и ..

Разностью двух векторов и , отложенных от одной точки является вектор, направленный из конца вычитаемого вектора в конец уменьшаемого вектора , т.е. (Рис. 4.2.). Это правило следует из формулы (1): т.к. , то .

Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры).

Вектор равен , где ‑ некоторое число, если:

1. 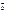коллинеарен ;

2.длина вектора отличается от длины вектора в раз, т.е. ;

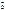1. при , и направлены в одну сторону, при ‑ в разные.

Произведение вектора на скаляр обладает следующими свойствами:

1. ;

2. ;

3. ;

4. ;

5. .

Не нашли, что искали? Воспользуйтесь поиском: