
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Линейные операции над матрицами.
1. Сложение матриц.
Суммой матриц А и В одинаковой размерности mXn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:
Свойства сложения:
1. А + В = В + А.
2. (А + В) + С = А + (В + С).
3. Если О – нулевая матрица, то А + О = О + А = А
Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.
Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.
2. Умножение матрицы на число.
Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.
Свойства умножения матрицы на число:
1. (km)A=k(mA).
2. k(A + B) = kA + kB.
3. (k + m)A = kA + mA.
Операции над матрицами
Суммой двух матриц  и
и  одинакового размера называется матрица
одинакового размера называется матрица  того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.  .
.
Сложение матриц обладает следующими свойствами:
1.Коммутативность, т.е.  .
.
2.Ассоциативность, т.е.  .
.
3.Для любых двух матриц  и
и  одинакового размера существует единственная матрица
одинакового размера существует единственная матрица  такая, что
такая, что  . Матрица
. Матрица  обозначается
обозначается  и называется разностью матриц
и называется разностью матриц  и
и  . Уравнение
. Уравнение  имеет решение
имеет решение 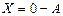 , получающаяся при этом матрица называется противоположной
, получающаяся при этом матрица называется противоположной  и обозначается
и обозначается  .
.
Произведением матрицы  на число
на число  называется матрица, все элементы которой равны соответствующим элементам матрицы
называется матрица, все элементы которой равны соответствующим элементам матрицы  , умноженным на число
, умноженным на число  .
.
Умножение матрицы на действительное число обладает следующими свойствами:
1.  ;
;
2.  ;
;
3.  ;
;
4.  (ассоциативность);
(ассоциативность);
5.  (дистрибутивность);
(дистрибутивность);
6.  (дистрибутивность).
(дистрибутивность).
Матрица  называется согласованной с матрицей
называется согласованной с матрицей  , если число столбцов матрицы
, если число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . В этом случае произведением матрицы
. В этом случае произведением матрицы 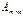 на матрицу
на матрицу  называется матрица
называется матрица 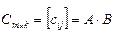 , где
, где 
 , т.е. элемент, стоящий в
, т.е. элемент, стоящий в  -той строке и
-той строке и  -том столбце матрицы произведения равен сумме произведений элементов
-том столбце матрицы произведения равен сумме произведений элементов  -той строки матрицы
-той строки матрицы  на соответствующие элементы
на соответствующие элементы  -го столбца матрицы
-го столбца матрицы  .
.
Свойства умножения:
1.Если матрица  согласована с матрицей
согласована с матрицей  , а матрица
, а матрица  согласована с матрицей
согласована с матрицей 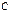 , то
, то  ‑ ассоциативность умножения;
‑ ассоциативность умножения;
2. 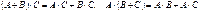 ‑ свойство дистрибутивности;
‑ свойство дистрибутивности;
3.Умножение матриц не коммутативно, т.е., как правило,  .
.
Обратная матрица
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А 1 , так что В = А 1 . Обратная матрица вычисляется по формуле  где А i j - алгебраические дополнения элементов a i j.
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы  обозначают
обозначают  или
или  .
.
Если все миноры порядка  данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы  ) равны нулю, то
) равны нулю, то  . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то
. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то  . Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка
. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 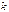 , окаймляющие ненулевой минор
, окаймляющие ненулевой минор  -го порядка равны нулю, либо таких миноров нет. Тогда
-го порядка равны нулю, либо таких миноров нет. Тогда  .
.
Не нашли, что искали? Воспользуйтесь поиском: