
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Однородные системы. Фундаментальная система решений. Неоднородные системы.
Критерий совместности системы линейных уравнений
Ответ на первый вопрос дает теорема Кронекера-Капелли – критерий совместности системы линейных уравнений.
Теорема. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Однородные системы уравнений
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:

Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что  не превосходит
не превосходит  . В случае
. В случае  система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при
система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при  .
.
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: Если у системы уравнений  , то ранг
, то ранг  системы не превышает числа уравнений
системы не превышает числа уравнений  , т.е.
, т.е.  . Таким образом, выполняется условие
. Таким образом, выполняется условие  и, значит, система имеет ненулевое решение.
и, значит, система имеет ненулевое решение.
Следствие 2: Однородная система  уравнений с
уравнений с  неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство: Допустим, система  линейных однородных уравнений, матрица которой
линейных однородных уравнений, матрица которой  с определителем
с определителем  , имеет ненулевое решение. Тогда по доказанной теореме
, имеет ненулевое решение. Тогда по доказанной теореме  , а это значит, что матрица
, а это значит, что матрица  вырожденная, т.е.
вырожденная, т.е.  .
.
Однородная система линейных алгебраических уравнений.
Система m линейных ур-ий с n переменными называется системой линейных однородных уравнений, если все свободные члены равны 0. Система линейных однородных ур-ий всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое решение. Система линейных однородных ур-ий имеет ненулевое решение тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. при rang A (n. Всякая лин. комбинация
решений системы лин. однородн. ур-ий также является решением этой системы.
Система лин.независимых решений е1, е2,…,еk называется фундаментальной, если каждое решение системы является линейной комбинацией решений. Теорема: если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменных n, то всякая фундаментальная система решений системы состоит из n-r решений. Поэтому общее решение системы лин. однордн. ур-ий имеет вид: с1е1+с2е2+…+сkеk, где е1, е2,…, еk – любая фундаментальная система решений, с1, с2,…,сk – произвольные числа и k=n-r. Общее решение системы m линейных ур-ий с n переменными равно сумме
общего решения соответствующей ей системы однородн. линейных ур-ий и произвольного частного решения этой системы.
7.Линейные пространства. Подпространства. Базис, размерность. Линейная оболочка. Линейное пространство  называется n-мерным, если в нем существует система из
называется n-мерным, если в нем существует система из  линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число
линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число  называется размерностью (числом измерений) линейного пространства
называется размерностью (числом измерений) линейного пространства  и обозначается
и обозначается  . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве
. Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве  найдется система, состоящая из
найдется система, состоящая из  линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:
линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:  ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность  линейно независимых векторов (базисных векторов).
линейно независимых векторов (базисных векторов).
Теорема 8.1 о разложении вектора по базису. Если  — базис n-мерного линейного пространства
— базис n-мерного линейного пространства  , то любой вектор
, то любой вектор 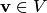 может быть представлен в виде линейной комбинации базисных векторов:
может быть представлен в виде линейной комбинации базисных векторов:
V=v1*e1+v2*e2+…+vn+en
и притом единственным образом, т.е. коэффициенты  определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства  равна
равна  . Система векторов
. Система векторов  линейно независима (это базис). После присоединения к базису любого вектора
линейно независима (это базис). После присоединения к базису любого вектора  , получаем линейно зависимую систему
, получаем линейно зависимую систему  (так как это система состоит из
(так как это система состоит из  векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
В самом деле, в пространстве  имеется система
имеется система  линейно независимых векторов, а любая система
линейно независимых векторов, а любая система 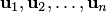 из большего количества векторов
из большего количества векторов  линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы
линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы  . Значит,
. Значит,  и
и  — базис
— базис  .
.
Не нашли, что искали? Воспользуйтесь поиском: