Евклидовы пространства. Норма вектора. Ортонормированный базис. Процесс ортогонализации. Неравенство Коши-Буняковского.

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно -мерное евклидово пространство обозначается , хотя часто используется не вполне приемлемое обозначение .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

где (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

,

где и .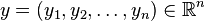

3. Вообще любое предгильбертово пространство (пространство со скалярным произведением ). Норма вектора [править | править исходный текст]

Норма в векторном пространстве над полем вещественных или комплексных чисел — это функционал , обладающий следующими свойствами:

1.

2. (неравенство треугольника);

3.

Эти условия являются аксиомами нормы.

Не нашли, что искали? Воспользуйтесь поиском: