
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лінійні перетворення, ранг і транспонування
Дії над матрицями
Операція порівняння
дві матриці  та
та  називаються рівними
називаються рівними  , якщо рівні їх відповідні елементи, тобто
, якщо рівні їх відповідні елементи, тобто  .
.
Додавання
Якщо дано дві матриці m -на- n A і B, можемо означити їх суму A + B як матрицю m -на- n, що утворюється додаваннямвідповідних елементів, себто,
(A + B)[ i, j ] = A [ i, j ] + B [ i, j ]. Наприклад,
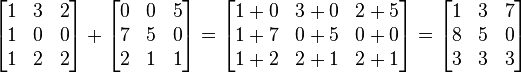
Множення на скаляр
Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[ i, j ] = cA [ i, j ].
З цими двома операціями множина M(m, n, R) усіх матриць m -на- n з дійсними елементами є дійсним векторним простором розмірності mn.
Множення матриць
Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m -на- n (m рядків, n стовпчиків), а B — матриця n -на- p (n рядків, p стовпчиків), їх добуток AB є матрицею m -на- p (m рядків, p стовпчиків), що розраховується за формулою:
(AB)[ i, j ] = A [ i, 1] * B [1, j ] + A [ i, 2] * B [2, j ] +... + A [ i, n ] * B [ n, j ] для кожної пари i та j
Це множення має такі властивості:
(AB) C = A (BC) для всіх матриць A розмірності k -на- m, B розмірності m -на- n і C розмірності n -на- p (асоціативність).
(A + B) C = AC + BC для всіх матриць A і B розмірності m -на- n і матриць C розмірності n -на- k (дистрибутивність).
C (A + B) = CA + CB для всіх матриць A і B розмірності m -на- n і матриць C розмірності k -на- m (дистрибутивність).
Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.
Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.
Лінійні перетворення, ранг і транспонування
Матриці можуть представляти лінійні перетворення, оскільки множення матриць відповідає композиції відображень, як це буде показано далі.
Надалі ототожнюватимемо R n з множиною рядків або матриць n -на-1. Для кожного лінійного відображення f: R n -> R m існує єдина матриця A розмірності m -на- n така, що f (x) = Ax для всіх x з R n. Кажемо, що матриця A "представляє" лінійне відображення f. Тепер, якщо матриця B розмірності k -на- m представляє інше лінійне відображення g: R m -> R k, лінійне відображення g o f представлене матрицею BA. Це випливає з зазначеної вище властивості асоціативності множення матриць.
Ранг матриці A — це розмірність образа лінійного відображення, представленого матрицею A. Вона збігається з розмірністю простору, згенерованого рядками матриці A, а також із розміром простору, згенерованого стовпчиками матриці A.
Транспонованою матрицею матриці A розмірності m -на- n є матриця A tr (також іноді позначають як A T або t A) розмірності n -на- m, яку одержують заміною рядків стовпчиками і навпаки, себто A tr[ i, j ] = A [ j, i ] для всіх індексів i та j. Якщо A описує лінійне відображення відносно двох базисів, матриця A tr описує транспозицію лінійного відображення відносно дуальних базисів, див. дуальний простір.
Маємо (A + B tr = A tr + B tr і (AB)tr = B tr * A tr.
Не нашли, что искали? Воспользуйтесь поиском: