Властивості визначників

1. Якщо помножити якийсь рядок на константу то визначник також помножиться на
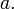
2. Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний.
3. При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться.
4. У матриці з двома однаковими/пропорційними рядками або з нульовим рядком, визначник дорівнює нулю.
5. Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців.
6. Визначник трикутної матриці дорівнює добутку елементів на діагоналі.
7. Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.
8. Лема про фальшивий розклад: сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.
9. 
10. 
11. 

В лінійній алгебрі доводиться, що перші три властивості майже характеризують визначник матриць з елементами у полі. А саме, якщо функція елементів матриці задовольняє 1,2,3, то така функція пропорціональна .

Обернена матриця

Обернена матриця — матриця (позначається ), яка існує для кожної невиродженої квадратної матриці , розмірності , причому:

де 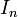одинична матриця.

Якщо для матриці існує , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.

Властивості

— операція обернення є інволюцією.

— обернення транспонованої матриці

— обернення спряженої матриці

для довільного коефіцієнта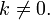

— визначник оберненої матриці.

— ранг матриці дорівнює розміру матриці.

Власні вектори матриці та її оберненої — збігаються, а власні значення є оберненими.

Якщо потрібно розв'язати систему лінійних рівнянь , (b — ненульовий вектор) і існує, тоді . В протилежному випадку або розмірність простору розв'язків більше нуля, або їх немає зовсім.

Приклади

Обернена матриця існує тоді і тільки тоді, коли .

7))) Система координат — спосіб задання точок простору за допомогою чисел.

Вектор

Геометричний вектор — у фізиці і математиці — величина, яка характеризується числовим значенням і напрямком. У фізиці існує чимало важливих величин, котрі є векторами, наприклад сила, положення, швидкість, прискорення, кутовий момент, імпульс, напруженість електричного і магнітного полів. Їх можна протиставити іншим величинам, таким, як маса, об'єм, тиск, температура та густина, які можна описати звичайним числом, їх називають «скалярами».

Графічно вектори зображають у вигляді напрямлених відрізків певної довжини . Наприклад, для графічного представлення сили величиною два ньютони треба намалювати відрізок прямої довжиною дві одиниці в напрямку дії сили. Стрілка вказує, що сила діє від точки A до точки B; якби сила діяла від B до A, то треба було б записати . Чисельне значення вектора називається модулем чи довжиною і позначається | |. Ця величина — скаляр. Два паралельних вектори, що мають однакові довжини, але протилежні напрямки, називаються протилежними. Якщо вектор позначено через , то протилежний йому вектор позначається через . Вектор, початок і кінець якого збігаються, називається нульовим і позначається .

Два вектори називаються рівними, якщо вони однієї довжини і їх напрямки збігаються. У механіці цим визначенням треба користуватися з обережністю, оскільки дві рівні сили, прикладені до різних точок тіла можуть призводити до різних результатів.

Багато алгебраїчних дій мають свої аналоги і для векторів: вектори можна між собою додавати і віднімати, можна множити і ділити на числа. Для цих операцій діють багато правил алгебри, як, наприклад, комутативність, асоціативність та дистрибутивність (віднімання трактується як особливий випадок додавання). Суму двох векторів з однаковим початком можна знайти геометрично за допомогою правила паралелограма.

Вектор є тензором першого рангу.

Не нашли, что искали? Воспользуйтесь поиском: