Відстань від точки до прямої на площині.

Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.

Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.

16))) Крива другого порядку - геометричне місце точок, декартові прямокутні координати яких задовольняють рівняння виду

в якому принаймні один з коефіцієнтів Багато важливих властивості кривих другого порядку можуть бути вивчені за допомогою характеристичної квадратичної форми, відповідної рівняння кривої

Так, наприклад, невироджених крива виявляється речовим еліпсом, уявним еліпсом, гіперболою або параболою в залежності від того, чи буде позитивно певної, негативно певної, невизначеною або полуопределенной квадратичною формою, що встановлюється по корінню характеристичного рівняння:

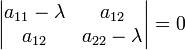
або

λ ² - I λ + D = 0.

Корені цього рівняння є власними значеннями речовій симетричної матриці

і, як наслідок цього, завжди речовинні.

відмінний від нуля.

Вид кривої	Канонічне рівняння	Інваріанти
Невироджені криві ()
Еліпс
Гіпербола
Парабола
Вироджені криві (Δ = 0)
Точка
Дві пересічні прямі
Дві паралельні прямі
Одна пряма	x 2 = 0

Для центральної кривої в канонічному вигляді її центр знаходиться на початку координат.

17)))) Площина - алгебраїчна поверхня першого порядку: у декартовій системі координат площина може бути задана рівнянням першого ступеня.

Загальне рівняння (повне) площині

де і 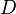- Постійні, причому і одночасно не дорівнюють нулю; в векторної формі:

де - Радіус-вектор точки , Вектор 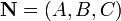перпендикулярний до площини (нормальний вектор). Напрямні косинуси вектора :

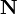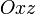Якщо один з коефіцієнтів в рівнянні площини дорівнює нулю, рівняння називається неповним. При площину проходить через початок координат, при (Або , ) П. паралельна осі (Відповідно або ). При (, Або ) Площина паралельна площині (Відповідно або ).

Рівняння площини у відрізках:

де , , - Відрізки, відсікаються площиною на осях і .

Рівняння площини, що проходить через точку перпендикулярно вектору нормалі :

у векторній формі:

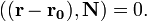
Рівняння площини, що проходить через три задані точки , Що не лежать на одній прямій:

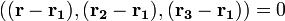
(Змішане твір векторів), інакше

Нормальне (нормоване) рівняння площини

у векторній формі:

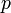де - Одиничний вектор, - Відстань П. від початку координат. Рівняння (2) може бути отримано з рівняння (1) множенням на нормуючий множник

(Знаки і 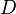протилежні).

18))))

Залежність змінної y від змінної х називається функцією, якщо кожному значення х відповідає єдине значення y. Змінну х називають незалежною змінною або аргументом, а змінну y – залежною змінною. Значення y, що відповідає заданому значенню х, називають значенням функції.

Не нашли, что искали? Воспользуйтесь поиском: