Границя функції на нескінченності і нескінченні границі

Нехай функція f(x) визначена при х > х₀ (х < х₀).

Визначення 5. Число А називається границею функції f(x) при х ®¥ (х ®-¥), якщо для будь-якого можна знайти таке , що при всіх х, які задовольняють нерівності 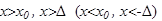, виконують нерівність

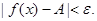
При цьому вживають відповідні позначення

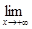f(x)=A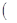 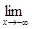f(x)=A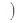

або

f(x)®A, х®+¥ (f(x)®A, х®-¥).

В разі, якщо існують границі функції f(x) як при х®+¥, так і при х®-¥, причому 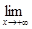f(x)= 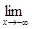f(x)=A 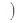, то вживають позначення

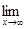f(x)=A або f(x)®A, х®¥

Вище малося на увазі, що А – певне число. Іноді зручно розглядати нескінченні границі функції.

Визначення 6. Кажуть, що функція f(x) має своєю границею +¥ (-¥) при х ® х₀ (або в точці х₀), якщо для будь-якого Е>0 можна знайти таке число δ>0, що при всіх х, які задовольняють нерівність 0<| x-x₀ |<δ, виконується нерівність f (x)> E (f (x)<- E).

При цьому вживають відповідно позначення

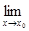f(x)= +¥ ( 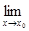f(x)=- ¥)

або

f(x)® +¥ х ® х₀ (f(x)®- -¥, х ® х₀).

Аналогічно тому, як це зроблено в 3.2 цього параграфа, нескладно визначити також односторонні нескінченні границі

f(x)= ±¥; 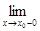f(x)=± ¥.

Приклад 5. Використовуючи визначення, довести 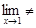(3 х -2)=1.

Δ Візьмемо будь-яке число ε >0. Задача полягає в тому, щоб по цьому ε знайти таке δ>0, при якому із нерівності | x -1|< δ випливала нерівність | f (x)-1|=|(3 x -2)-1|< ε. Перетворюючи останню нерівність, отримаємо |(3 x -1|< ε або | x -1|< .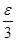

Отже, якщо взяти δ 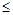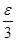, то для всіх х, які задовольняють нерівності | x -1|< δ, виконується нерівність | f (x)-1|< ε. Це і означає, що 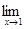=(3 х -2)=1.

Якщо, наприклад, ε =1, то δ≤ 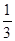, якщо ε = 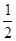, то δ≤ 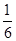, якщо ε =0,01, то δ≤0,03 і т.д.; таким чином, δ залежить від ε. Тому в визначенні границі іноді пишуть δ= δ(ε).

22))) Нескінченно мала (величина) - числова функція або послідовність, яка прагне до нуля.

Нескінченно велика (величина) - числова функція або послідовність, яка прагне до нескінченності певного знака.

1. Обчислення нескінченно малих і великих

Обчислення нескінченно малих - обчислення, вироблені з нескінченно малими величинами, при яких похідний результат розглядається як нескінченна сума нескінченно малих. Обчислення нескінченно малих величин є загальним поняттям для диференціальних і інтегральних обчислень, що становлять основу сучасної вищої математики. Поняття нескінченно малої величини тісно пов'язано з поняттям межі.

1.1. Нескінченно мала величина

Послідовність a _n називається нескінченно малою, якщо 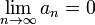. Наприклад, послідовність чисел 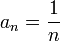- Нескінченно мала.

Функція називається нескінченно малою в околиці точки x ₀, Якщо .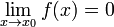

Функція називається нескінченно малою на нескінченності, якщо або .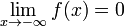

Також нескінченно малою є функція, що є різниця функції та її межі, тобто якщо 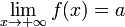, То f (x) - a = α (x), .

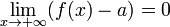1.2. Нескінченно велика величина

У всіх наведених нижче формулах нескінченність праворуч від рівності мається на увазі певного знаку (або "плюс", або "мінус"). Тобто, наприклад, функція x sin x, Необмежена з обох сторін, не є нескінченно великою при .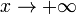

Послідовність a _n називається нескінченно великою, якщо .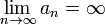

Функція називається нескінченно великою в околиці точки x ₀, Якщо .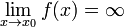

Функція називається нескінченно великою на нескінченності, якщ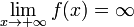о або .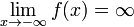

Не нашли, что искали? Воспользуйтесь поиском: