Основні теореми про границю

Теорема 2.11. Границя сталого дорівнює сталому, тобто

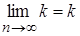, де .

Доведення. Нехай , де . Розглянемо різницю , маємо: – нескінченно мала величина. За теоремою 2.4 маємо, що .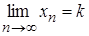

Теорема 2.12. Границя суми дорівнює сумі границь.

Доведення. Нехай, наприклад, , . Покажемо, що . Дійсно

За оберемо 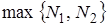та оцінимо модуль , маємо:

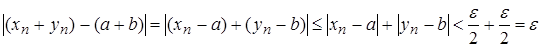.Таким чином,

.

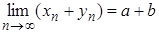Зауваження. Випадок суми довільного скінченного числа числових послідовностей доводиться аналогічно.

Теорема 2.13. Границя добутку дорівнює добутку границь.

Доведення. Нехай, наприклад, , . Покажемо, що 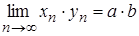. Дійсно, якщо , то за теоремою 2.3 , де – нескінченно мала величина. Аналогічно, 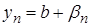, де – нескінченно мала. Тоді

.

Оскільки константа є величиною обмеженою, то за теоремою 2.6 величини є нескінченно малими; за теоремою 2.5 величина 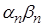також є нескінченно малою. Оскільки сума трьох нескінченно малих величин є нескінченно малою, то 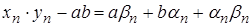є нескінченно мала і за теоремою 2.4.

Зауваження

1) Сталий множник можна виносити за знак границі.

Дійсно,

.

2) .

Дійсно,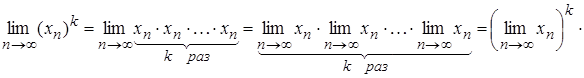

3) .

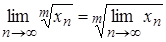Теорема 2.14. Границя частки двох послідовностей дорівнює частці границь цих послідовностей, якщо границя знаменника не дорівнює нулю, тобто

, де .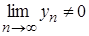

Зауваження. Доведення даної теореми проводиться аналогічно доведенню теореми 2.13.

Теорема 2.15.

1) 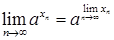, де ;

2) , де .

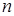
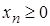Теорема 2.16. Якщо для послідовності відомо, що для всіх і , то .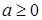

Доведення. Проведемо доведення методом від супротивного. Нехай , але тод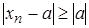і і 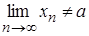. Остання рівність суперечить умові теореми. Це означає, що наше припущення хибне і .

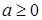Теорема 2.17. Якщо для послідовностей та 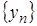відомо, що , то .

Доведення. За умовою теореми , тоді за теоремою 2.16

.

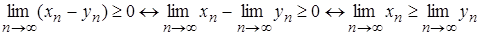Теорема 2.18. .

Важливі границі

Перша чудова границя -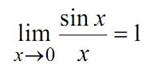

Друга чудова границя -

Не нашли, что искали? Воспользуйтесь поиском: