Область визначення і область значень функції

Область визначення функції - це множина всіх значень змінної x, при яких функція має зміст.

З'ясуємо, як знайти область визначення деяких функцій, заданих формулою.

1. Якщо функція — многочлен, то вона існує при будь-яких значеннях аргумента, тобто її область визначення — всі дійсні числа.

2. Якщо функція задана формулою, яка містить аргумент у знаменнику дробу, то до області визначення функції входять всі дійсні числа, крім тих, які перетворюють знаменник в нуль.

3. Якщо функція задана формулою, яка містить арифметичний квадратний корінь, то до області її визначення входять всі дійсні числа, при яких підкореневий вираз набуває невід'ємних значень.

Область значень функції (множина значень) - усі значення, яких набуває функція.
Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)
Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)

\ 19))) Елементарні функції та їх класифікація

Показникова функція (рис.5.3).

Функція означена в інтервалі і неперервна в кожній точці цього інтервалу. При функція зростає; при - спадає. Областю зміни показникової функції є інтервал .

Логарифмічна функція (рис.5.4).

Функція означена в інтервалі і неперервна в кожній точці цього інтервалу. При функція зростає; при - спадає.

Область зміни логарифмічної функції складає множина всіх дійсних чисел.

Степенева функція (рис.5.5, 5.6).

Якщо відносно відомо лише, що це деяке дійсне число, то можна говорити про значення тільки для . Тому в загальному випадку областю означення степеневої функції вважають інтервал . Якщо то означена і в точці , де приймає значення . При зростанні степенева функція зростає, якщо і спадає, якщо . Значення у степеневої функції заповнюють інтервал . Якщо число - ціле або дробове з непарним знаменником, то степенева функція при означена для всіх , а при - для всіх , крім .

Тригонометричні функції (рис.5.7, 5.8, 5.9, 5.10).

Функці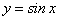ї і мають областю визначення всі

значення змінної . Множиною значень кожної з цих функцій є

відрізок .

Функція означена для всіх значень , крім . Множина значень: .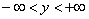

Функція означена для всіх значень , крім . Множина значень: .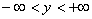

Обернені тригонометричні функції (рис.5.11, 5.12, 5.13, 5.14).

- нескінченнозначна функція, обернена для функції . Область означення: ; область зміни 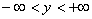. Якщо кожному значенню покласти у відповідність значення нескінченнозначної функції , що задовольняє умовам , одержимо однозначну функцію, яку будемо позначати і називати головним значенням функції .

Функція - нескінченнозначна, обернена для функції . Область означення: ; область зміни: 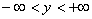. Якщо кожному значенню , покласти у відповідність значення нескінченнозначної функції , що задовольняє умовам , одержимо однозначно функцію, яку будемо позначати і називати головним значенням функції .

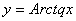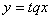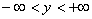Функції і - нескінченнозначні, обернені відповідно для функцій і . Області означення: ; області зміни: 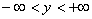, крім відповідно

і .

Якщо кожному значенню , , 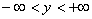поставити у відповідність значення функції , що задовольняють нерівностям , то одержимо функцію, яку назвемо головним значенням багатозначної функції і будемо позначати .

Не нашли, что искали? Воспользуйтесь поиском: