Знаходження похідних вищих порядків

Під похідною вищих порядків розуміють диференціювання функції більше ніж один раз. Якщо похідну 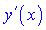повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції , і вона позначається

Похідна третього порядку матиме запис

Аналагічно отримують формули для знаходження похідних вищих порядків. При знаходженні похідної порядку необхідно знати похідну -го порядку. Вийняток становлять функції, для яких можна помітити закономірність зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:

В інших випадках, для знаходження похідних вищих порядків від заданої функції потрібно послідовно знаходити всі її похідні нижчих порядків. Для практичного вивчення матеріалу розглянемо приклади.

Похідні вищих порядків

Нехай функція f (х) задана на деякому проміжку (a; b) і нехай всередині цього проміжку вона має похідну f ' (х). Тоді може статися так, що f ' (х), будучи функцією від х, у деякій точці х ₀Î (a; b), а можливо, і в усіх точках цього проміжку, в свою чергу, має похідну. Цю похідну називають похідною другого порядку, або другою похідною від функції f (х) в точці х ₀.

Похідна другого порядку позначається одним із таких символів: у "; f "(х ₀)

Отже, за означенням, похідна другого порядку це є похідна першого порядку від похідної першого порядку, тобто у " = (у ')'.

Звідси випливає таке правило знаходження похідної другого порядку.

Щоб знайти від функції у = f (х) похідну другою порядку, треба знайти спочатку від цієї функції похідну першого порядку у', а потім від похідної у' знайти ще похідну першого порядку.

31)) Диференціал функції

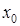Нехай функція має в даній точці скінченну похідну . Тоді , де , якщо . Звідки

.

Якщо 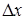- нескінченно малий приріст, то доданок 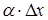є нескінченно малим вищого порядку, ніж доданок і якщо , то і 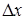-нескінченно малі одного порядку.

Означення 3.3. Якщо функція має похідну 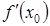в точці 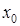, то вираз називається диференціалом (differential) функції в цій точці і позначається символом 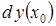. Тобто,

. (3.10)

Зауваження. Диференціал функції в даній точці є головною лінійною частиною приросту функції, пропорційною приросту аргументу з коефіцієнтом пропорційності :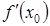

.

Диференціал незалежної змінної ототожнюється з її приростом, тобто

.

Для будь-якої диференційовної в точці х функції формулу (3.10) можна записати так:

.

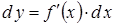Звідки отримаємо, що

тобто похідну можна розглядати як відношення двох диференціалів.

Не нашли, что искали? Воспользуйтесь поиском: