Диференціювання функцій, заданих параметрично

Нехай функції і параметрично задають функцію , причому і - функції диференційовні за змінною t і .

Похідну від функції y за змінною x знаходимо, диференціюючи і за змінною t (див. формулу (*)):

, .

Тоді

,

тобто

. \

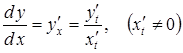32))) Диференціали вищих порядків

Нехай для функції існує диференціал першого порядку:

.

Означення 1. Диференціалом другого порядку функції називається диференціал від диференціала першого порядку і позначається , тобто .

Аналогічно, і т.д.

І взагалі, диференціалом -го порядку називається диференціал від диференціала -го порядку, тобто

.

За означенням

Отже, якщо - незалежна змінна, то . Аналогічно, .

З останньої формули маємо, що при довільному

,

тобто похідну -го порядку функції можна записати як відношення її диференціала -го порядку до -го степеня диференціалу аргумента.

Приклад. Знайти , якщо .

,

А тоді .

Ми вже показали, що диференціал першого порядку інваріантний відносно форми, а диференціали вищих порядків такої властивості не мають.

Теорема 1. Диференціали вищих порядків не зберігають форму.

Доведення. Розглянемо випадок . Нехай функції та мають похідні до другого порядку включно. Тоді , де - диференціал, а не приріст (). Звідки

,

що й потрібно було довести.

Не нашли, что искали? Воспользуйтесь поиском: