Теорема Коші про середнє значення

Теорема, що належить французькому математикові Огюстену Коші й називається узагальненою теоремою про скінченні прирости. Вона узагальнує теорему Лагранжа.

Якщо кожна з двох функцій та неперервна на проміжку та диференційована в усіх внутрішніх точках цього проміжка і якщо, окрім того, похідна відмінна від нуля скрізь у проміжку , то на цьому проміжку знайдеться точка така, що має місце формула:

.

Формулу (1) називають узагальненою формулою скінченних приростів, або формулою Коші.

Доведення

Перш за все покажемо, що . І справді, якщо б це було не так, то для функції на проміжку були б виконані умови теореми Ролля. Тоді б на проміжку знайшлася б точка така, що . Останнє протирічить умові теореми. Отже, , і ми маємо право розглянути наступну допоміжну функцію:

В силу умов, які накладено на функції та , функція неперервна на проміжку та знайдеться точка така, що

Маючи на увазі те, що

,

і використовуючи рівність (3) отримаємо:

Враховуючи, що з рівності (4) отримуємо формулу Коші:

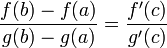
Теормему доведено.

Зауваження

Формула Лагранжа є частковим випадком формули Коші (1), коли .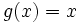

У формулі (1) зовсім не обов'язково вважати, що

Теорема про середнє значення

Визначений інтеграл дорівнює добутку довжини відрізка інтегрування на значення підінтегральної функції в деякій точці відрізка:
(3.27)Значення функції f(c) називається середнім на проміжку (а, в). Згідно (3.27) маємо:
(3.28)Поняття середнього значення функції використовується в різноманітних сферах науки і техніки, позаяк багато величин часто характеризуються своїми середніми значеннями. Наприклад, середня швидкість хімічної реакції, середня потужність змінного струму, середній тиск та інші.
34)))) Пра́вило Лопіта́ля — у математичному аналізі — метод знаходження границь функції, розкриття невизначеностей вигляду і . Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функцій дорівнює границі частки їхніх похідних.

Точне формулювання

Правило говорить, що якщо функції і задовольняють такі умови:

або ;

;

в проколотому околі ;

Якщо і — диференційовані в проколотому околі ,

то існує . При цьому теорема вірна і для інших баз (для вказаної буде наведено доказ).

Відношення нескінченно малих

Доведемо теорему для випадку, коли границі функцій дорівнюють нулю (т.з. невизначеність вигляду ).

Оскільки ми розглядаємо функції і лише у правому проколотому півоколі точки , ми можемо неперервним чином їх довизначити в цій точці: нехай . Візьмемо деякий з даного півоколу і застосуємо до відрізку теорему Коші. За цією теоремою отримаємо:

,

але , тому .

Далі, записавши визначення границі функції відношення похідних і позначивши останню через , з отриманої рівності виводимо:

для скінченної границі і

для нескінченої,

що є визначенням границі відношення функцій.

Відношення нескінченно великих

Доведемо теорему для невизначеностей вигляду .

Нехай, для початку, границя відношення похідних скінченна і рівна . Тоді, при прямуванні до справа, це відношення можна записати як , де — O(1). Запишемо цю умову:

.

Зафіксуємо з відрізка і застосуємо теорему Коші до всіх з відрізка :

, що можна привести до такого вигляду:

.

Для , достатньо близьких до , вираз має межу першого множника правої частини рівний одиниці (так як і — константи, а і прямують до безмежності). Значить, цей множник рівний , де — нескінченно мала функція при прямуванні до справа. Випишемо визначення цього факту, використовуючи те ж значення , що і в визначенні для :

.

Отримали, що відношення функцій можна подати у вигляді , і . По будь-якому данному можна знайти таке , щоб модуль різниці відношення функцій і був менше , значить, границя відношення функцій дійсно рівна .

35))) Монотонна функція - це функція, прирощення якої не змінює знака, тобто або завжди невід'ємне, або завжди непозитивно. Якщо на додаток прирощення не дорівнює нулю, то функція називається строго монотонним. Монотонна функція - це функція, що змінюється в одному і тому ж напрямку.

Функція зростає, якщо більшому значенню аргументу відповідає більше значення функції. Функція убуває, якщо більшому значенню аргументу відповідає менше значення функції.

1. Визначення

Нехай дана функція Тоді

функція f називається зростаючою на M, Якщо

.

функція f називається строго зростаючої на M, Якщо

.

функція f називається спадною на M, Якщо

.

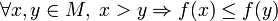функція f називається строго спадною на M, Якщо

.

(Строго) зростаюча або спадна функція називається (строго) монотонною.

2. Інша термінологія

Іноді зростаючі функції називають неубутною, а убуваючі функції невозрастающімі. Строго зростаючі функції тоді звуть просто зростаючими, а строго убуваючі просто убутними.

3. Властивості монотонних функцій

Монотонна функція, визначена на інтервалі, вимірна щодо борелевскіх сигма-алгебр.

Монотонна функція, визначена на замкнутому інтервалі, обмежена. Зокрема, вона інтегрована по Лебегу.

Монотонна функція може мати розриви тільки першого роду. Зокрема, безліч точок розриву не більше ніж лічильно.

Монотонна функція дифференцируема майже всюди щодо заходи Лебега.

4. Умови монотонності функції

(Критерій монотонності функції, що має похідну на інтервалі) Нехай функція неперервна на (A, b), і має в кожній точці похідну f '(x). Тоді

f зростає на (A, b) тоді і тільки тоді, коли

f убуває на (A, b) тоді і тільки тоді, коли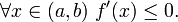

(Достатня умова суворої монотонності функції, що має похідну на інтервалі) Нехай функція неперервна на (A, b), і має в кожній точці похідну f '(x). Тоді

якщо то f строго зростає на (A, b);

якщо то f строго убуває на (A, b).

Зворотне, взагалі кажучи, невірно. Похідна строго монотонною функції може звертатися в нуль. Однак, безліч точок, де похідна не дорівнює нулю, має бути щільно на інтервалі (A, b). Точніше має місце

(Критерій суворої монотонності функції, що має похідну на інтервалі) Нехай 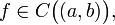і всюди на інтервалі визначена похідна f '(x). Тоді f строго зростає на інтервалі (A, b) тоді і тільки тоді, коли виконані наступні дві умови:

Аналогічно, f строго убуває на інтервалі (A, b) тоді і тільки тоді, коли виконані наступні дві умови:

Екстремуми функцій

Точка х₀ називається точкою локального максимуму функції , якщо для будь-яких досить малих виконується нерівність

.

Точка х₀ називається точкою локального мінімуму функції , якщо для будь-яких досить малих виконується нерівність

.

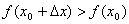Точки максимуму і мінімуму називаються точками екстремуму функції , а значення функції в екстремальних точках – її екстремальними значеннями.

Необхідну ознаку локального екстремуму дає така теорема:

Теорема 1. Якщо функція має в точці х₀ локальний екстремум, то 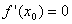або , або не існує.

Проте виявляється, що цього недостатньо, бо може 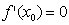, а функція в цій точці екстремуму не має.

Точки, в яких функція визначена та неперервна, і в цих точках або не існує, називаються критичними для функції.

Проте не в кожній критичній точці функція має екстремум. Тому потрібні достатні ознаки існування екстремуму для функції f. Їх дають такі теореми:

Теорема 2.

Нехай функція неперервна в деякому інтервалі, який містить критичну точку х₀, і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки х₀).

Якщо для х<х₀ , а для х₀<x , то для х=х₀ функція має максимум.

Якщо для х<х₀ , а для х₀<x , то для х=х₀ функція має мінімум.

Теорема 3.

Нехай функція два рази диференційована в околі точки х₀ і 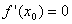. Тоді в точці х=х₀ функція має локальний максимум, якщо , і локальний мінімум, якщо .

Якщо ж , то точка х=х₀ може й не бути точкою екстремуму.

Звідси випливає такий план знаходження екстремальних точок:

1. знаходять критичні точки функції , тобто точки, в яких , або не існує;

2. знаходять другу похідну і обчислюють значення другої похідної в цих точках.

Якщо значення другої похідної в критичній точці від’ємне, то така точка є точкою максимуму, а якщо значення другої похідної додатне, то точка є точкою мінімуму.

Якщо в критичній точці, то нічого конкретного сказати не можна, бо в цій точці може бути екстремум, а може й не бути.

Не нашли, что искали? Воспользуйтесь поиском: