Числа їх класифікація.Узагальнення множини дійсних чисел.

Число́ — міра кількості чогось.У давнину "число" означало "знак", "символ", "поняття".Під словом "числити" розуміли в ті часи "значити", "думати", а також "записувати щось за допомогою знаків", "робити певні дії зі знаками". Натуральні числа(1,2,3 і т.д.)Дослівно - "природні" числа. Натуральні числа - найдавніші числа, які стали використовувати люди, в першу чергу при лічбі: Сукупність всіх натуральних чисел позначається –N Цілі числа-Назва "цілі числа" виникла на противагу дробам. Цілі числа утворюються на основі натуральних за допомогою введення нових понять і позначень: нуля та від'ємних чисел.Від'ємні числа позначаються за допомогою знака мінус. У множині цілих чисел (на відміну від натуральних) завжди здійсненне віднімання.Множина цілих чисел позначається - z. Раціональні числа назва - "дроби", тобто числа, якими можна позначити нецілу кількість предметів - півтора, третину стакана, чверть години і тощо. Під дробовими числами, як правило, розуміють ті раціональні числа, які не відносяться до цілих..У множині раціональних чисел (на відміну від цілих) завжди здійснене ділення, крім ділення на 0. Множина всіх раціональних чисел позначається -Q.Дійсні числа-Назва чисел відображає думку про те, що вони дають змогу описувати дійсність (реальність). Сукупність раціональних та ірраціональних чисел утворює множину дійсних чисел.Найбільш поширене позначення дійсних чисел - у вигляді десяткових (можливо нескінченних) дробів. У множині дійсних чисел (на відміну від раціональних) завжди здійсненна дія добування кореня натурального степеня зневід'ємного числа.Множина дійсних чисел позначається-R,.Комплексні числа-Дослівний переклад назви цих чисел - "складені" ("складні") числа, Кожне комплексне число можна трактувати як пару дійсних чисел; якщо другий елемент цієї пари рівний 0, то таке комплексне число ототожнюють з дійсним Ті комплексні числа, які не ототожнені з жодним дійсним числом, називаються уявними числами У множині комплексних чисел завжди здійсненна дія добування кореня довільного натурального степеня з довільного комплексного числа Як наслідок, стає можливим розв'язати довільне квадратне рівняння (тобто навіть з від'ємним дискримінантом).Комплексні числа плідно використовуються також для розв'язування кубічних рівнянь (за формулами Кардано). Множина комплексних чисел позначається -c

2) Число a+bi, де a і b – будь-які дійсні числа, i – уявна одиниця, називається комплексним числом (a – дійсна частина,bi – уявна частина комплексного числа, а b – коефіцієнт при уявній частині).Число, квадрат якого дорівнює -1, позначають буквою I, і називають уявною одиницею (i – перша буква латинського слова imaginarius – уявний).Слово "комплексний" означає складений.Часто комплексне число позначають буквою z і записують z=a+bi.Комплексні числа – це розширення числової системи дійсних чисел. Позначаються вони буквою c. Два комплексних числа a+bi і c+di рівні між собою тоді і тільки тоді, коли a=c і b=d, тобто, коли рівні їх дійсні частини і коефіцієнти при уявних частинах. Числа a+bi та a-bi, дійсні частини яких рівні, а коефіцієнти при уявих частинах рівні за модулем, але протилежні за знаком, називають спряженими.Числа a+bi та –a-bi, називаються протилежнимиДії над ними:а) Додавання:.Сумою двох комплексних чисел і називається комплексне число , дійсна частина якого і коефіцієнт при уявній частині дорівнюють відповідно сумі дійсних частин і коефіцієнтів при уявних частинах додатків.б) Віднімання комплексних чисел.Різницею двох комплексних чисел і називається комплексне.число .в) Множення комплексних чисел.Добутком двох комплексних чисел і називається комплексне.число 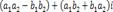.г) Ділення комплексних чисел.Часткою комплексних чисел і називається комплексне число .Д)Піднесення до степеня. 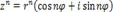Е)Добування кореня.

3) Множина́ — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Множина вважається означеною, якщо про кожен об'єкт, що розглядається, можна казати, що він або належить, або не належить множині. Ідентичні (тобто однакові) об'єкти в множині не допускаються. Безліч зазвичай позначають великими латинськими літерами, а елементи множини - малими латинськими літерами.Якщо елемент, а належить множині А, то пишуть: а А, а якщо а неналежить А,то пишутьа А. Способи завдання безлічі
Безліч А вважається заданим, якщо стосовно будь-якого об'єкта а можна встановити, належить цей об'єкт безлічі А чи не належить; іншими словами, якщо можна визначити, чи є а елементом множини А чи не є. Існують два основних способи завдання множини: 1) перелік елементів множини; 2) вказівку характеристичного властивості елементів множини, тобто такої властивості, яке мають усі елементи даної множини і тільки вони.
Першим способом особливо часто задаються скінченні множини. Наприклад, безліч студентів навчальної групи задається їхнім списком. Безліч, що складається з елементів a, b, c,..., d, позначають за допомогою фігурних дужок: А = {a; b; c;...; d}. Безліч коренів рівняння х ^2-5х +6 = 0 складається з двох чисел 2 і 3: А = {2; 3}. Безліч У цілих рішень нерівності -2 <х <3 складається з чисел -1, 0, 1, 2, тому В = {-1, 0, 1, 2}.
Другий спосіб завдання множини є більш універсальним. Безліч елементів х, що володіють даними характеристичним властивістю Р (х), також записують за допомогою фігурних дужок: Х= {х | Р (х)}, і читають: безліч Х складається з елементів х, таких, що виконується властивість Р (х) Дії над ними:А)Об'єднання множин
Об'єднанням А. У множин А і В називається множина, яка складається з усіх елементів, що належать хоча б одній з множин А чи В. Б) Перетин множин
Перетином А ∩ В множин А і В називається множина, яка складається з усіх елементів, що належать одночасно кожному з множин А і ВВ) Різниця множин
Різницею А \ У множин А і В називається множина, яка складається з усіх елементів множини А, які не належать безлічі В, тобто Г) Доповнення множини
Нехай безліч А і В такі, що А 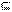В. Тоді доповненням множини А до множини В називається різниця В \ А. У цьому випадку застосовується позначення С _B А = В \ А. Якщо в якості безлічі У береться універсальне безліч U, то застосовується позначення СА = С _U А = U \ А і таке безліч просто називають доповненням множини А. Таким чином, символічна запис визначення доповнення безлічі буде наступною: СА = {x | x 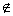A}. 4) Комбінаторика вивчає питання про те, скільки різних комбінацій, підпорядкованих тим чи іншим умовам, можна скласти із заданих об’єктів. Розміщенням із n елементів по m називається любий впорядкований набір із m різних елементів, вибраних із загальної сукупності в nелементів.При цьому можуть бути розміщення без повторень , коли два набори вважаються різними,якщо вони відрізняються один від одного хоча б одним елементом, або коли набори однакові по складу, - порядком розташування цих елементів в наборі.В цьому випадку справедливе співвідношення де n! = 1•2•3•...•n,(n - m)! = 1•2•3•...•(n - m).В розміщеннях з повтореннями 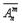в набір можуть входити і однакові елементи,але набори також відрізняються один від одного або складом елементів, або порядком розміщення цих елементів в них.Доведено, що 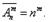Перестановками із n елементів називається любий впорядкований набір цих елементів.В перестановках без повторень

набори містять n елементів із n і відрізняютьсяодин від одного лише порядком елементів в них.Очевидно, що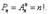

Комбінацією із n елементів по m називається любий невпорядкований набір із m різних елементів, вибраних із загальної сукупності в nелементів.В комбінаціях без повторень 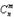набори відрізняються один від одного лише складомі розраховуються по формулі

5)Відсотком якого-небудь числа називають соту частину цього числа. Відношення суми, яку виплачують за користування грошовими засобами до величини грошових засобів називають питомою відсотковою ставкою(і)I=w/100%Це саме відношення виражає відсоткова ставка Якщо при вкладанні засобів відсоток від них додається до початкових засобів – мова йде йде про нагромадження. Якшо на добавлений відсоток не нарах. Нові відсотки то мова йде про прості відсотки. Нехай початковий капітал фірми – К01 –питама ставка, івідсотокнараховано протягом тр- тоді нагром. За цей період кінцевий капітал обчислюють Км=К0(1+ i*m) Прості відцьотки при цьому = К0 *i*m Такою формулою фінансові установи встановлюючи певно к-сть річ. Відсох. З подальшим поділом по місяцях (днях)

6)Часто крім простих відсотків використовують складні відсотки які відрізняються що в кожному наступному періоді відсоток буде обчислю. Від суми в яку вже включені відсотки за попередній період. Ms =Ks =K0 (1 +i) в степені s (формула розрах. Кінц. Капіталу при складних відсотках) 1+і =r коефіцієнт складного відсотка Ks=K0 +rв степені s. Формули для розрахунку простих і складних відсотків вважають найпростішими економічними мат. Моделями що використовують фін. Установи і банки. Як правило складні відсотки добавляється 1 раз на рік але можна робити розрах і за менші періоди часу (корот. Терм. Кредит.).Нехай К0 відс. Склад. –і, кількість років m, відсоток nрозрах 1 раз на рік доті кінц. Капіт Km=K0(1+1/n)в степеніm*n. Якщо протягом рівних періодів часу на рах. Вноситься постійна сума то таки. Вклад – періоди. Вклад під складні %.Кінцевий капітал можна розрах як суму геометр. Прогрес.. S=Km=K0r * r(в степені m)-1 / (r-1)

7)З розрахунком простих і складних % повязують питання дискотування. Коли треба знайти початк. Капітал на основі кінцевого.Дисконтування – основна процедура фінансових операцій, лежить в основі доходності фінансових ринків. Дисконтування є єдиною методикою, яка порівнює вартість різних об‘єктів у часі. Дисконтування приводить теперішню вартість до майбутньої і навпаки. Дисконтування може проводитися різними методами.Різницю Km-K0=Q-дисконтом. Проблему дискотування зустрічають коли необхідно визначити активність капіталовкладень. Коефіцієнтом дисконту називають величину Ʋ= 1/r

8 питання. Метод координат

Методкоординат- спосібвизначати положенняточкиабо тілаза допомогоючиселабоіншихсимволів (наприклад, положення шаховихфігурнадошцівизначається за допомогоючиселібукв). Числа(символи), що визначають положенняточки(тіла) на прямій,площині,впросторі, на поверхні ітакдалі, називаються їїкоординатами.Залежновід цілей іхарактеру дослідженнявибираютьрізні системикоординат. Вектором називають напрямлений відрізок. А – початок вектора, В- кінець вектора.Вектор позначається a або AB. Абсолютною величиною (або модулем) вектора називається довжина відрізка, що зображає вектор.Абсолютна величина вектора a позначається |a|.Два вектори називаються рівними, якщо вони суміщаються паралельним перенесенням.Рівні вектори однаково напрямлені і рівні за абсолютною величиною.Рівні вектори мають рівні відповідні координати.Якщо у векторів координати рівні, то вектори рівні. Координатами вектора a називають числа a₁ = x₂ - x₁, a₂ = y₂ - y₁,де A₁(x₁, y₁), A₂(x₂, y₂) - кінці вектора a. Сумою векторів a i b з координатами (a₁, a₂) і (b₁, b₂) називається вектор с з координатами (a₁ + b₁, a₂ + b₂), тобто a(a₁, a₂) + b(b₁, b₂) = c(a₁ + b₁, a₂ + b₂). Різницею векторів a і b з координатами (a₁, a₂) і (b₁, b₂) називається вектор с з координатами (a₁-b₁, a₂-b₂), тобто a(a₁, a₂) - b(b₁, b₂) = c(a₁ - b₁, a₂ - b₂). Добутком вектора a на число λ називається вектор с з координатами (λa₁, λa₂), тобтоλa(a₁, a₂) = c(λa₁, λa₂). Абсолютна величина вектора λa дорівнює |λ||a|.Напрям вектора λa, збігається з напрямом вектора a, якщо λ > 0, і протилежний напряму вектора a, якщо λ < 0. Два вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.У колінеарних векторів відповідні координати пропорційні. Скалярним добутком векторів a(a₁, a₂) i b(b₁, b₂) називається число a₁b₁ + a₂b₂.Кутом між ненульовими векторами AB i AC називається кут BAC.
Кутом між будь-якими двома векторами a i b називається кут між векторами, що дорівнюють даним і мають спільний початок.Кут між однаково напрямленими векторами дорівнює нулю.Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними: a•b = |a|•|b|•cos φ. Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.Якщо скалярний добуток векторів дорівнює нулю, то вектори перпендикулярні.Векторним добутком вектора на вектор називають вектор С, який задовольняє таким трьом умовам:1) модуль вектора С обчислюють за формулою: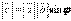

.

9 питання Лінія і пряма на площині

Не нашли, что искали? Воспользуйтесь поиском: