
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Означення неперервності в точці за Гейне
Функція f називається неперервною в точці 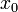 якщо:
якщо: 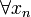 , якщо
, якщо  , то
, то  .
.
Точки розривуТочка розриву - це така точка (значення аргументу) в якій функція не є неперервною.Розрізняють такі види точок розриву:Розрив називають усувним, якщо в даній точці існує границя функції, що не збігається з значенням функції.
Точку називають точкою розриву першого роду, якщо існують скінченні ліва та права границі в даній точці, та вони не збігаються.Якщо хоча б одна одностороння границя не існує, чи нескінченна, то точку називають точкою розриву другого роду.

Якщо границі функцій F(x) і G(x) при х, що прямує до х0 існують і є скінченними, то виконуються правила:- границя суми цих функцій дорівнює сумі їх границь;- границя різниці цих функцій дорівнює різниці їх границь;- границя добутку цих функцій дорівнює добутку їх границь;- границя відношення цих функцій дорівнює відношенню їх границь, якщо границя дільника відмінна від нуля.Для того щоб знайти границю елементарної функції, коли аргумент прямує до значення, що належить області визначення функції, треба замість аргумента в вираз підставити граничне значення аргументу. Це правило називається правилом граничного переходу.
23)Функція fix) називається нескінченно малою при х —> a, якщо lim fix) = 0.х—>аФункція f(x) називається нескінченно великою при х —> a, якщо limf(x) = оо, або1іт/(х) = -оо, або1іт/(х) = +оо.х—>а х—>а х—>аРозглянемо властивості нескінченно малих і нескінченно великих функції.1. Якщо фушщїі/(х) і g(x) - нескінченно малі при х —> a, то їх cyMa/(xj + g(x) прих —> а також є нескінченно малою функцією.2. Якщо фушщїі/(х)- нескінченно мала прих —> a,aF(x) - обмежена функція, то їх добугок f(x)-F(x)) прих —> а також є нескінченно малою функцією.Наслідок: Добугок скінченого числа нескінченно малих функцій є величина нескінченно мала.3.Якщо при х —> а фушщія/(х) має скінчену границю lim f(x) = A, а функціяx—>а….g(x) - нескінченно велика, то lim(/(x) + g(x)) = оо, lim = 0.4. Між нескінченно великими і нескінченно малими величинами існує простий зв'язок: якщо х нескінченно велика величина, то 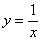 — нескінченно мала, і навпаки, якщо у — нескінченно мала і у
— нескінченно мала, і навпаки, якщо у — нескінченно мала і у  0, то
0, то 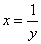 буде нескінченно великою величиною.Тому можна довести, що алгебраїчна сума скінченної кількості нескінченно великих величин буде величиною нескінченно великою, добуток нескінченно великої величини на обмежену величину також буде нескінченно великою величиною.
буде нескінченно великою величиною.Тому можна довести, що алгебраїчна сума скінченної кількості нескінченно великих величин буде величиною нескінченно великою, добуток нескінченно великої величини на обмежену величину також буде нескінченно великою величиною.
24…1 Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границявідношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною. Геометричний зміст похідноїЗначення похідної  функції
функції 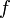 у точці
у точці 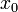 дорівнює значення кутового кофіціента дотичної до кривої
дорівнює значення кутового кофіціента дотичної до кривої  у точці з абсцисою
у точці з абсцисою 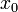 .Рівняння дотичної до кривої
.Рівняння дотичної до кривої  у точці M(
у точці M( ) має вигляд:
) має вигляд:  y=f́(x)=tga 1 Геометричний зміст поняття похідної
y=f́(x)=tga 1 Геометричний зміст поняття похідної
Нехай на площині x0y дана безперервна крива y = f (x) (див. рис. 1).
Розглянемо на графіку кривої точки M o (x o; f (x o)) і M 1 (x o + D x; f (x o + D x)). Проведемо січну M o M 1. Нехай - Кут нахилу січної M o M 1 щодо осі 0х. Якщо існує межа
, То пряма, що проходить через M o і утворює з віссю 0х кут
, Називається дотичною до графіка даної кривої в точці M o. Таким чином, під дотичної до кривої y = f (х) в точці M o природно розуміти граничне положення січної M o M 1, до якого вона прагне, коли D x ® 0.
Нехай N (x o + D x; f (x o)) - точка, яка доповнює відрізок M o M 1 до прямокутного трикутника M o M 1 N. Оскільки сторона M o N паралельна осі 0 х, то
Переходячи до границі в лівій і правій частинах цього рівності при D x → 0, отримаємо
Тому геометричний зміст похідної полягає в тому, що f '(x 0) - це тангенс кута нахилу (кутовий коефіцієнт) дотичній до графіка y = f (х) в точці (x o; f (x o)). Фізичний зміст похідноїПохідна від шляху за часом дорівнює миттєвій швидкості руху матеріальної точки Механічний зміст похідної: величина миттєвої швидкості в момент часу t0 дорівнює значенню похідної від шляху у точці t0. Використовується поняття еластичності функції.
Означення: Еластичністю функції Еx (y) називається границя відношення відносного приросту функції у до відносного приросту змінної х при  х à 0:
х à 0: 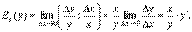 Еластичнісіь функції наближено відображає, на скільки відсотків зміниться функція у = f (х) при зміні незалежної змінної х на 1%.
Еластичнісіь функції наближено відображає, на скільки відсотків зміниться функція у = f (х) при зміні незалежної змінної х на 1%.
25 Диференціалом функції f (х) в точці х 0 називається лінійна функція збільшення виду
Диференціал функції y = f (х) позначається dy або df (x 0). Головне призначення диференціала полягає в тому, щоб замінити прирощення на лінійну функцію від
, Зробивши при цьому, по можливості, меншу помилку. Наявність кінцевої похідної
дає можливість уявити приріст функції
у вигляді
де
при
. З цього випливає, що помилка в наближеному рівність
(Рівна
) Є нескінченно малою більш високого порядку, ніж
, Коли
. Це часто використовують при наближених обчисленнях основні формули диф-нняПрактично ж похідні функцій знаходять за основними правила-ми та основними формулами диференціювання. Основні правила диференціювання:1.(С)' = 0.2.(х)'х =1.3.(u + v-w)' = u'x+v'x-w'x.4.(Cu)' = C-u'x.5.(uv)' = u'xv + uv'x.
26.1. Похідна постійної величини С=0, тобто С’=0.2.Похідна алгебраїчної суми функцій=такій самій алгебраїчній сумі їх похідних-[f1(x)±f2(x)±…. ±fn(x)]’=f1’(x) ±f2’(x) ±…..± fn’(x)(3.якщо кожна з функцій u(x) та v(x) диференційована в точці х, то добуток цих функцій також має похідну в точці х[u(x)*v(x)]’=u’(x)*v(x) =u(x)*v’(x)4.якщо u(x) та v(x) мають похідні в точці х і v (x)≠0, то частка цих функцій має похідну в точці х…Нехай функція має похідну 1 –го порядку і є визначеною. Тоді її похідна y’=f(x)’ буде похідною 2-го порядку. Похідну 2-го порядку позначають f’’(x) або y’’. Аналогічно визначаються похідні третього, четвертого порядків. Похідні вищих порядків мають широке застосування. так якщо функція S=S(t) описує закон руху матеріальної точки, то її перша похідна S’(t) – величина миттєвої швидкості, а друга похідна S’’(t) – прискорення в момент t.
27.
Знаходимо похідну f’(x) заданої функції
1. Знаходимо критичні точки(f’(x)=0)
2. Визначаємо знак f’(x) в кожному інтервалі
3. Робимо висновок(зростання, спадання)
4. Обчислюємо максимальне та мінімальне значення ф-ції.
5. Приклад у=2  -9
-9  +12х+7 y’=6
+12х+7 y’=6  -18x+12
-18x+12
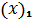 =1
=1  =2
=2  =
=  =
=
29. Крива y=f(x) – опукла на інтервалі (a,b), якщо усі точки графіка ф-ції лежать нижче її дотичних на цьому інтервалі.
Крива y=f(x) – угнута на інтервалі (a,b), якщо усі точки графіка ф-ції лежать вище її дотичних на цьому інтервалі.
Якщо в досить малому околі точки дотику  крива зліва цієї точки лежить по один бік дотичної, а справа – з іншого боку дотичної, то точку х=
крива зліва цієї точки лежить по один бік дотичної, а справа – з іншого боку дотичної, то точку х=  називають точкою перегину кривої.
називають точкою перегину кривої.
Точка х=  буде точкою перегину кривої у=f(x), якщо:f’’(
буде точкою перегину кривої у=f(x), якщо:f’’( )=0 або не існує. знаки f(x) зліва (х<
)=0 або не існує. знаки f(x) зліва (х<  ) та справа (х>
) та справа (х>  ) різні приклад y=
) різні приклад y=  +4
+4  y’=4
y’=4  +12
+12  y’’=12
y’’=12  +24x
+24x
12  +24x=0
+24x=0
x(12x+24)=0
x=0 або 12х+24=0
12х=-24
Х=-2
(-2;0) – інтервал опуклості
(  - інтервали угнутості.
- інтервали угнутості.
30) Найбільше і найменше значення функції
Багато практичних задач зводяться до знаходження найбільших або найменших значень деяких функцій на певних проміжках. При цьому важливу роль відіграє таке твердження: якщо функція неперервна на деякому проміжку, то серед її значень на цьому проміжку є найбільше і найменше.
Схема знаходження найбільшого і найменшого значень функції на проміжку така:
- Знайдіть похідну функції і її критичні точки;
- Знайдіть значення функції на кінцях проміжку;
- Знайдіть значення функції в критичних точках, які належать заданому проміжку;
- З усіх знайдених значень функції оберіть найбільше і найменше.
Для розв’язання практичних задач спочатку складають аналітичний вираз для тієї функції, за допомогою якої одна величина виражається через другу, після чого знаходять найбільше або найменше значення одержаної функції.
При цьому користуються такою схемою:
- Оберіть одну зі змінних (незалежну змінну) і складіть через неї функцію (залежну змінну), для якої знаходять найбільше або найменше значення;
- Знайдіть проміжок зміни незалежної змінної;
- Знайдіть похідну функції, яку склали;
- Прирівняйте похідну функції до нуля і знайдіть корені отриманого рівняння;
- Знайдіть точки, в яких похідна не існує;
- Знайдіть значення функції на кінцях проміжку зміни незалежної змінної і в точках, де похідна не існує або дорівнює нулю;
- Оберіть зі знайдених значень найбільше або найменше.
. Знаходження найбільшого і найменшого значень функції.Щоб знайти найбільше (найменше) значення неперервної функції на відрізку, треба знайти максимуми і мінімуми і порівняти їх із значеннями функції, яких вона набуває на кінцях відрізка. Найбільше (найменше) число серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку  . Приклад. Знайти найбільше і найменше значення функції
. Приклад. Знайти найбільше і найменше значення функції  на відрізку.
на відрізку.
Р о з в ’я з о к. Знаходимо стаціонарні точки. Для цього обчислимо похідну  Прирівнюючи цю похідну до нуля і розв’язуючи рівняння дістаємо стаціонарні точки.Точок, в яких похідна не існує, немає.Обчислимо значення функції в точках), а також на кінцях відрізкаМаємо
Прирівнюючи цю похідну до нуля і розв’язуючи рівняння дістаємо стаціонарні точки.Точок, в яких похідна не існує, немає.Обчислимо значення функції в точках), а також на кінцях відрізкаМаємо

Отже, найбільше значення становить 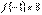 , найменше -
, найменше - 
 Щоб знайти найбільше (найменше) значення функції
Щоб знайти найбільше (найменше) значення функції  замкненій області
замкненій області  , потрібно знайти значення функції у всіх критичних точках і порівняти їх з найбільшими (найменшими) значеннями функції на границях області: найбільше і найменше із цих значень і буде найбільшим і найменшим значенням функції в даній області.
, потрібно знайти значення функції у всіх критичних точках і порівняти їх з найбільшими (найменшими) значеннями функції на границях області: найбільше і найменше із цих значень і буде найбільшим і найменшим значенням функції в даній області.
31) Поняття функції двох і більше змінних. Область визначення. Ізолінії.На практиці досить часто функція y залежить не від однієї змінної x, а від багатьох аргументів x 1,…, x n. Означення. Множина значень { x 1,…, x n}, за яких вираз f (x 1,…, x n) має зміст, називається областю визначення функції від n змінних y = f (x 1,…, x n). Приклади. 1. Функція від двох змінних z =3 x +5 xy + y 2. Область визначення цієї функції - всі пари дійсних чисел (x; y).2. Функція від чотирьох змінних y =2 x 1+3 x 2- x 3+7 x 4.3. Функція від трьох змінних V=V (a, b, c)= a×b×c. Об’єм паралелепіпеда є функцією від довжин його сторін.4. Функція від двох змінних Q = F (K, L). Обсяг випущеної продукції Q є функцією від кількості затраченого капіталу K та кількості затраченої праці L. Областю визначення цієї функції є множина { K ³0; L ³0}.5. Область визначення функції  визначається з нерівності 100- x 2- y 2³0, тобто x 2+ y 2£102. Це круг з центром у початку координат і радіусом r = 10.Функція від двох змінних (аргументів) f(x, y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції
визначається з нерівності 100- x 2- y 2³0, тобто x 2+ y 2£102. Це круг з центром у початку координат і радіусом r = 10.Функція від двох змінних (аргументів) f(x, y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції  є верхня половина сфери (рис. 6.1).
є верхня половина сфери (рис. 6.1).
 z
z
 |



 6 8 10 y
6 8 10 y
x
Рис. 6.1.
Функції від двох змінних геометрично зображають також за допомогою ліній рівня (ліній однакового рівня, ізоліній). Означення. Лінією рівня функції від двох змінних z = f (x, y) називається множина точок площин OXY таких, що f (x, y)=const= C. Прикладом ізоліній є паралелі та меридіани. Приклади. 1. Побудуємо лінії однакового рівня функції  . При C =0 маємо
. При C =0 маємо  тобто x 2+ y 2=102 (коло з радіусом r =10, рис.6.2).При C =6 отримуємо
тобто x 2+ y 2=102 (коло з радіусом r =10, рис.6.2).При C =6 отримуємо  тобто x 2+ y 2=82. Отже лінією рівня, яка відповідає константі C =6, є коло з радіусом r = 8.При C =8 отримуємо ізолінію (неявну функцію y від x) x 2+ y 2=62.
тобто x 2+ y 2=82. Отже лінією рівня, яка відповідає константі C =6, є коло з радіусом r = 8.При C =8 отримуємо ізолінію (неявну функцію y від x) x 2+ y 2=62.

 y
y
 |
6 8 10 x
Рис. 6.2.
2. Для випуску продукції Q використовують ресурси x 1 та x 2. Виробнича функція має вигляд Q =10 x 1+20 x 2 (ресурси повністю взаємозамінні, наприклад, цвяхи та шурупи).
Зобразити ізолінії для Q=Q (x 1, x 2) (лінії однакової кількості продукції, ізокванти).
Очевидно, що при C =60 ізолінія (ізокванта) – це відрізок прямої 10 x 1+20 x 2=60, а при C =40 – відрізок прямої 10 x 1+20 x 2=40 (рис. 6.3).

(Ресурс x 1)
 4 Q =60
4 Q =60
 3
3

 2 Q =40
2 Q =40
 1
1
 1 2 3 4 5 6 (Ресурс x 2)
1 2 3 4 5 6 (Ресурс x 2)
Рис. 6.3.
.
Не нашли, что искали? Воспользуйтесь поиском: