
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Неперервність функцій двох змінних
Означення. Функція 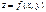 називається неперервною в точці
називається неперервною в точці 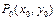 , якщо
, якщо 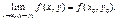 Означення. Функція
Означення. Функція 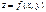 неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області. Означення. Функцію
неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області. Означення. Функцію  , визначену на множині
, визначену на множині 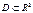 , називають неперервною за множиною
, називають неперервною за множиною 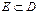 в точці
в точці 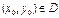 , якщо
, якщо  Означення. Точка
Означення. Точка 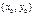 називається точкою розриву функції
називається точкою розриву функції  , якщо:функція
, якщо:функція  не визначена в точці
не визначена в точці 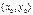 ;
;  функція
функція  не визначена в точці
не визначена в точці 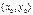 , проте:
, проте: 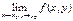 не існує;
не існує; 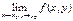 існує, але не дорівнює
існує, але не дорівнює 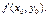 Означення. Точка
Означення. Точка 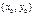 називається точкою усувного розриву функції
називається точкою усувного розриву функції  , якщо
, якщо 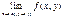 існує, але або
існує, але або 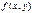 не визначена в точці
не визначена в точці 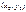 , або
, або 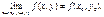 Неперервність складеної (складної) функції двох зміннихОзначення. Нехай функція
Неперервність складеної (складної) функції двох зміннихОзначення. Нехай функція 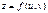 визначена на множині
визначена на множині 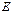 ,а змінні
,а змінні  і
і  , у свою чергу, залежать від змінних
, у свою чергу, залежать від змінних  і
і 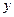 :
: 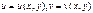 , причому обидві функції
, причому обидві функції 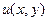 та
та 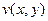 визначені на множині
визначені на множині  . Якщо для будь-якого
. Якщо для будь-якого  існує значення
існує значення 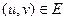 , то говорять, що на множині визначено складену (складну) функцію
, то говорять, що на множині визначено складену (складну) функцію 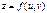 де
де 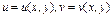 ;
;  ,
,  --проміжні,
--проміжні,  ,
, 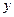 --незалежні змінні. Приклад. Функція
--незалежні змінні. Приклад. Функція 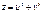 , де
, де  Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді
Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді
 Теорема 1.6. нехай на множині
Теорема 1.6. нехай на множині  визначено складену функцію
визначено складену функцію 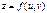 , де
, де  і нехай функції
і нехай функції 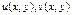 неперервні в точці
неперервні в точці  , а функція
, а функція 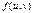 неперервна в точці
неперервна в точці  , де
, де  Тоді складена функція
Тоді складена функція  неперервна в точці
неперервна в точці  . Доведення. За умовою теореми функція
. Доведення. За умовою теореми функція 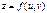 неперервна. За означенням неперервності функції в точці
неперервна. За означенням неперервності функції в точці 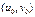 візьмемо довільне число
візьмемо довільне число 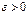 , тоді існує
, тоді існує 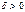 , що з нерівності
, що з нерівності 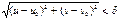 (5)випливає нерівність
(5)випливає нерівність 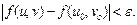 Аналогічно функції
Аналогічно функції 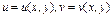 за умовою теореми неперервні, тому існують такі
за умовою теореми неперервні, тому існують такі 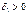 і
і  , що з нерівностей
, що з нерівностей 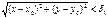 і
і 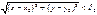 випливають нерівності
випливають нерівності
 (6),(7)
(6),(7)
Нехай 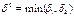 . Тоді з нерівності
. Тоді з нерівності
 (8)дістанемо нерівності (6) і (7).З урахуванням нерівностей (6) і (7) для нерівності (5) запишемо:
(8)дістанемо нерівності (6) і (7).З урахуванням нерівностей (6) і (7) для нерівності (5) запишемо:  .Отже, якщо виконується нерівність (8), маємо
.Отже, якщо виконується нерівність (8), маємо  ,а це означає, що складена функція
,а це означає, що складена функція 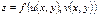 неперервна в точці
неперервна в точці 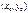 .
.
Не нашли, что искали? Воспользуйтесь поиском: