
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Бачимо, що різниця між повною та частковою похідними полягає у виключенні непрямих залежностей між змінними в останній.
Тепер припустимо, що з певних причин пропорції конуса мають залишитись сталими, і відношення між висотою та радіусом стале: k:
Це дає повну похідну: Рівняння, що містять часткові похідні, називають рівняннями в часткових похідних, і вони часто використовуються у фізиці, інженерії та інших науках і прикладних дисциплінах.
35) повний диференціал його геометричний зміст приклади.Поняття диференціала тісно пов'язане з поняттям похідної, і е одним з найважливіших в математиці. Диференціал наближено дорівнює приросту функції і пропорційний приросту аргументу. Внаслідок цього диференціал широко застосовується при дослідженні різноманітних процесів і явищ. Будь-який процес протягом достатньо малого проміжку часу змінюється майже рівномірно, тому дійсний приріст величини, що характеризує процес, можна замінити диференціалом цієї величини на даному проміжку часу. Таку заміну називають лінеаризацією процесу.Термін «диференціал» (від латинського слова differentia - різниця) ввів у математику Лейбніц. 1. Означення, геометричний та механічний зміст диференціала.Нехай функція у = f (х) диференційовна в точці х [а; b], тобто в цій точці має похідну.Тоді з властивості 1o (гл. 4, п. 3.6)при х 0,звідки(1)Перший з доданків лінійний відносно х і при х 0 та f' (х) 0 є нескінченно малою одного порядку з х, тому що (гл. 4, п. 4.3):Другий доданок - нескінченно мала вищого порядку, ніж х, тому що.Цей доданок не є лінійним відносно х, тобто містить х в степені, вищому від одиниці. Таким чином, перший доданок у формулі (1) є головною частиною приросту функції, лінійною відносно приросту аргументу.Диференціалом dy функції у = f (х) в точці х називається головна, лінійна відносно х, частина приросту функції f(х) в цій точці:dy = f' (х) х. (2).Диференціал dy називають також диференціалом першого порядку. Якщо у = х, то у' = х' = 1, тому dy = dx = х, тобто диференціал dx незалежної змінної х збігається з її приростом х. Тому формулу (2) можна записати так:dy = f'(x)dx. (3).Формула (4) дає змогу розглядати похідну як відношення диференціала функції до диференціала незалежної змінної.Зауважимо, що коли в точці х0 похідна f' (х0) = 0, то перши й доданок у формулі (1) дорівнює нулеві і вже не є головною частиною приросту. Але і в цьому випадку диференціал dy знаходять за формулою (4).Геометричний зміст диференціала зрозумілий з рис. 5.18. Маємо.PN =y, QN = MNtg=хf'(x) = f'(x)dx = dy.Отже, диференціал функції f (х) при заданих значеннях х і х дорівнює приросту ординати дотичної до кривої у = f (х) в точці х. Приріст функції y при цьому дорівнює приросту ординати кривої. Таким чином, заміна приросту функції на її диференціал геометрично означає заміну ординати АР кривої ординатою дотичної AQ. Зрозуміло, що така заміна доцільна лише для достатньо малих значень х.З'ясуємо механічний зміст диференціала. Нехай матеріальна точка рухається за відомим законом S = f(t), де f(t) - диференційовна на деякому проміжку функція. Тоді диференціал цієї функції dS = f'(t) при фіксованих значеннях t і - це той шлях, який пройшла б матеріальна точка за час, якби вона рухалась прямолінійно і рівномірно із сталою швидкістю. Зрозуміло, що фактичний шлях S у випадку нерівномірного руху на відміну від диференціала dS не є лінійною функцією часу і тому відрізняється від шляху dS. Проте якщо час достатньо малий, то швидкість руху не встигає суттєво змінитись, і тому рух точки на проміжку часу від t до t + є майже рівномірним.Поняття диференціала можна проілюструвати і на інших прикладах, які розглянуто в п. 1.1. У кожному з них поняття диференціала набуває конкретного фізичного змісту.
36)Так як частинні похідні характеризують швидкість зміни функції у напрямі паралельному до одног з осей кординат,то можна знаходити похідну у довільному напрямку задано прямою L.Похыдна за напрямом позначаэться dz/dl - називається границею відношення приросту функції в даному напрямку,до відповідного зміщення dz/dl=limдельта f(x;y)/s.градієнтом - функції двох змінних наз вектор(grad),який в якості координат має частинні похідніgrad=(dz/dx; dz/dy)Градієнт вказує напрям вздовж якого функція зростає найбільше
37)Диф.рівняння 2-го порядку наз- диф.рівняння,яке містить 2 гу похідну.Найпрстішим є диф.рівняння із сталими кофіцієнтами y''+py'+qy=f(x)-неоднорідне.Якщо f(x)=0,то y''+py'+qy=0 -однорідне 2 - го порядку p'q-const/Порядок розвязку1)Складаємо характер диф рівняння виду y''=r^2,(^-означає до квадрату)r^2+pr+q=x..y=C1y1+C2y2=C1e^r1x+C2e^r2x//2) Якщо задана умова Коші,то для диф.рівняння необхідно знайти константи С1 і С2а)Взяти похідну від загального розвязкуб)Підставити умову Коші рівняння у загальне і похіднув)Розвязати систему рівняння
38)Матриця Гессе — квадратна матриця елементами якої є часткові похідні деякої функції.
Формально, нехай дано дійсну функцію від n змінних: 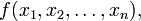 якщо у функції f існують всі похідні другого порядку, то можна визначити матрицю Гессе для цієї функції:
якщо у функції f існують всі похідні другого порядку, то можна визначити матрицю Гессе для цієї функції: 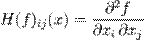
де 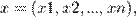 тобто
тобто 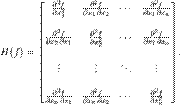
Визначник цієї матриці називається визначником Гессе, або гессіаном.
Значення матриці Гессе пояснюється її появою у формулі Тейлора:
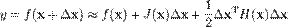 Матриці Гессе використовуються в задачах оптимізації методом Ньютона. Повне обчислення матриці Гессе може бути досить складним, тому були розроблені квазіньютонівськіалгоритми, засновані на наближених виразах для матриці Гессе. Найвідоміший з них — алгоритм Бройдена - Флетчера - Гольдфарба - Шанно. Змішані похідні функції f — це елементи матриці Гессе, що стоять не на головній діагоналі. Якщо вони неперервні, то порядок диференціювання не важливий:
Матриці Гессе використовуються в задачах оптимізації методом Ньютона. Повне обчислення матриці Гессе може бути досить складним, тому були розроблені квазіньютонівськіалгоритми, засновані на наближених виразах для матриці Гессе. Найвідоміший з них — алгоритм Бройдена - Флетчера - Гольдфарба - Шанно. Змішані похідні функції f — це елементи матриці Гессе, що стоять не на головній діагоналі. Якщо вони неперервні, то порядок диференціювання не важливий: 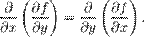 Це можна також записати як
Це можна також записати як 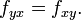 В цьому випадку матриця Гессе є симетричною.Якщо градієнт
В цьому випадку матриця Гессе є симетричною.Якщо градієнт 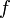 (її векторна похідна) рівний нулю в деякій точці
(її векторна похідна) рівний нулю в деякій точці 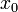 , то ця точка називається критичною.якщо матриця Гессе є додатноозначеною в точці
, то ця точка називається критичною.якщо матриця Гессе є додатноозначеною в точці 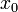 , то
, то 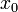 — точка локального мінімуму функції
— точка локального мінімуму функції 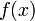 ,якщо матриця Гессе є від'ємноозначеною в точці
,якщо матриця Гессе є від'ємноозначеною в точці 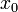 , то
, то 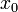 — точка локального максимуму функції
— точка локального максимуму функції 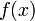 ,якщо матриця Гессе не є ні додатноозначеною ні від'ємноозначеною і невироджена
,якщо матриця Гессе не є ні додатноозначеною ні від'ємноозначеною і невироджена 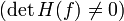 , то
, то 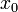 — сідлова точка функції
— сідлова точка функції 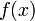 .
.
39) Теорема. Нехай в околі критичної точки  функція
функція 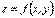 має неперервні частинні похідні до другого порядку включно. Розглянемо вираз
має неперервні частинні похідні до другого порядку включно. Розглянемо вираз 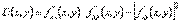 . Тоді)1) якщо
. Тоді)1) якщо 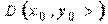 , то в точці
, то в точці  функція
функція 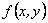 має екстремум; максимум, якщо
має екстремум; максимум, якщо 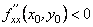 , і мінімум, якщо
, і мінімум, якщо 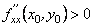 ,2) якщо
,2) якщо  , то в точці
, то в точці  функція
функція 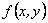 екстремуму не має.У випадку, коли
екстремуму не має.У випадку, коли  , екстремум в точці
, екстремум в точці  може бути, може і не бути. Приклад. Знайти екстремум функції Р о з в ’ я з о к. Знаходимо критичні точки функції
може бути, може і не бути. Приклад. Знайти екстремум функції Р о з в ’ я з о к. Знаходимо критичні точки функції  :Функція має дві критичні точки:
:Функція має дві критичні точки: 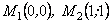 . Знаходимо частинні похідні другого порядку: Дослідимо характер першої критичної точки
. Знаходимо частинні похідні другого порядку: Дослідимо характер першої критичної точки  :
:  .Отже, в точці
.Отже, в точці 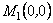 функція не має ні максимуму, ні мінімуму.Дослідимо характер другої точки
функція не має ні максимуму, ні мінімуму.Дослідимо характер другої точки 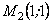 :
: 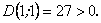 Оскільки
Оскільки 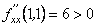 , то в точці
, то в точці 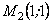 функція має мінімум:
функція має мінімум: 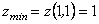 .
.
40) У багатьох задачах потрібно знаходити екстремуми функції, аргументи якої задовольняють деяким додатковим умовам – зв’язку. В цих випадках аргументи функції не є незалежними. Екстремуми такого типу називаються умовними. Теорема Лагранжа (про скінченні прирости функції). Нехай задано функцію f (х), неперервну на відрізку [ a, b ] і диференційовну на інтервалі (а і b).Тоді-знайдеться-точка x (а < x < b), така що похідна f¢ (x) функції в цій точці f¢ (x) дорівнюватиме відношенню 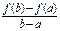 :
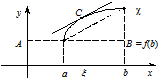
:  Геометрична інтерпретація теореми Лагранжа. На інтервалі (a, b) знайдеться хоча б одна точка x, в якій дотична є паралельною хорді АВ, що сполучає кінці дуги функції f (x) на відрізку [ a, b ]
Геометрична інтерпретація теореми Лагранжа. На інтервалі (a, b) знайдеться хоча б одна точка x, в якій дотична є паралельною хорді АВ, що сполучає кінці дуги функції f (x) на відрізку [ a, b ]
41) Функція 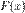 зветься первісною функції
зветься первісною функції 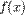 на деякому інтервалі дійсних чисел, якщо
на деякому інтервалі дійсних чисел, якщо 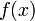 — похідна функції
— похідна функції 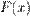 на цьому інтервалі, тобто в усіх внутрішніх точках інтервалу виконується рівність
на цьому інтервалі, тобто в усіх внутрішніх точках інтервалу виконується рівність
 10. Похідна від невизначеного інтеграла дорівнює підінтегральній функції:
10. Похідна від невизначеного інтеграла дорівнює підінтегральній функції: 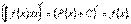 20. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу
20. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу 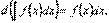 Ця рівність отримується на основі властивості 2030.
Ця рівність отримується на основі властивості 2030.  Цю рівність легко перевірити диференціюванням.40. Постійний множник можна виносити за знак інтеграла
Цю рівність легко перевірити диференціюванням.40. Постійний множник можна виносити за знак інтеграла 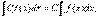 с
с  - константа.50. Інтеграл алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів з окремих доданків:
- константа.50. Інтеграл алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів з окремих доданків: 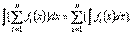 60. Якщо
60. Якщо 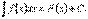 то
то  - довільні константи.
- довільні константи.
1Таблиця. 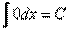 .2
.2 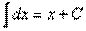 3)
3) 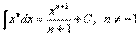 4.
4.  .5.
.5. 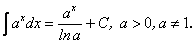 6.
6. 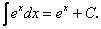 7.
7. 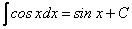 .
.
Метод підстановки
В методі підстановки (замiни змiнної) вводиться нова змінна, зв'язана із початковою змінною x певним співвідношенням. Якщо позначити цю змінну t, то співвідношення заміни змінної запишеться у вигляді 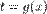 . Відповідно, для диференціалів
. Відповідно, для диференціалів 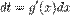 . Тоді
. Тоді 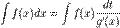 .В цей вираз потрібно підставити змінну х через змінну t. Якщо підстановку вибрати правильно, то загальний вираз спроститься. Приклад Нехай потрібно взяти інтеграл
.В цей вираз потрібно підставити змінну х через змінну t. Якщо підстановку вибрати правильно, то загальний вираз спроститься. Приклад Нехай потрібно взяти інтеграл 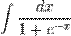 Вводимо нову змінну
Вводимо нову змінну  . Тоді
. Тоді  . Інтеграл переписується
. Інтеграл переписується
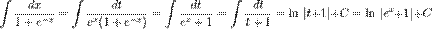 Метод інтегрування частинами В цьому методі використовується властивість
Метод інтегрування частинами В цьому методі використовується властивість 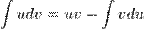 ,де u і v - деякі функції підінтегральної змінної. Вдале застосування цієї властивості дозволяє спростити інтегрування Приклад Нехай потрібно взяти інтеграл
,де u і v - деякі функції підінтегральної змінної. Вдале застосування цієї властивості дозволяє спростити інтегрування Приклад Нехай потрібно взяти інтеграл
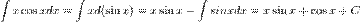 Метод безпосереднього інтегруванняЦей метод базується на рівності, де а та b – де сталі і застосовується у тих випадках, коли підінтегральна функція f має вигляд однієї із підінтегральних функцій табличних інтегралів, але її аргумент відрізняється від змінної інтегрування постійним доданком або постійним множником або постійним множником та постійним доданком.
Метод безпосереднього інтегруванняЦей метод базується на рівності, де а та b – де сталі і застосовується у тих випадках, коли підінтегральна функція f має вигляд однієї із підінтегральних функцій табличних інтегралів, але її аргумент відрізняється від змінної інтегрування постійним доданком або постійним множником або постійним множником та постійним доданком. 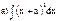
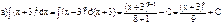
43) Визначеним інтегралом функції називається границя послідовності інтегральних сум при наближенні до нуля довжини найбільшого частинного інтервалу, якщо ця границя існує і не залежить від способу розбиття на елементарні відрізки і від вибору проміжних точок. Теорема існування визначеного інтеграла.Якщо функція f(x) неперервна в замкненому інтервалі [a,b], то її інтегральна сума прямує до границі при прямуванні до нуля довжини найбільшого частинного інтервалу.Ця границя (тобто визначений інтеграл) не залежить від способу розбиття на елементарні відрізки і від вибору проміжних точок.Нехай функція f неперервна на відрізку [а, b] та F — певна первісна для f на цьому відрізку, тоді: 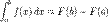 Ця формула називається формулою Ньютона—Лейбніца. Іноді її називають основною формулою інтегрального числення. Для скорочення запису часто застосовуеться позначення:
Ця формула називається формулою Ньютона—Лейбніца. Іноді її називають основною формулою інтегрального числення. Для скорочення запису часто застосовуеться позначення: 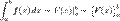
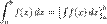 Формула Ньютона-Лейбніца для обчислення визначеного інтегралу є узагальненням методу Архімеда для обчислення площ і поверхонь плоских, криволінійних поверхонь, об'ємів тіл, довжин кривих та інших задач.1. Визначений інтеграл є мірою площі.Визначений інтеграл J/(x)afc дорівнює площі криволінійної трапеції.2)При переставленні меж інтегрування, визначений інтеграл змінює знак, не змінюючи абсолютної величини.3) Поділ відрізка інтегрування. 4) Знак визначеного інтеграла 5)Визначений інтеграл суми функцій надається як алгебраїчна сума інтегралів. 6)Сталий множник можна виносити за знак визначеного інтеграла
Формула Ньютона-Лейбніца для обчислення визначеного інтегралу є узагальненням методу Архімеда для обчислення площ і поверхонь плоских, криволінійних поверхонь, об'ємів тіл, довжин кривих та інших задач.1. Визначений інтеграл є мірою площі.Визначений інтеграл J/(x)afc дорівнює площі криволінійної трапеції.2)При переставленні меж інтегрування, визначений інтеграл змінює знак, не змінюючи абсолютної величини.3) Поділ відрізка інтегрування. 4) Знак визначеного інтеграла 5)Визначений інтеграл суми функцій надається як алгебраїчна сума інтегралів. 6)Сталий множник можна виносити за знак визначеного інтеграла
44 ). а) якщо на відрізку [a;b] функція f(x)>=0, то площа криволінійної трапеції обчислюється за формулою: S= 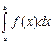 б) якщо на відрізку [a;b] функція f(x)<=0, то площа криволінійної трапеції обчислюється за формулою: S=
б) якщо на відрізку [a;b] функція f(x)<=0, то площа криволінійної трапеції обчислюється за формулою: S= 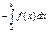 в) якщо фігура обмежена лініями функції y= f1(x) і y= f2(x) (причому f1(x) >f2(x)), то площа фігури обчислюється за формулою:S=
в) якщо фігура обмежена лініями функції y= f1(x) і y= f2(x) (причому f1(x) >f2(x)), то площа фігури обчислюється за формулою:S= 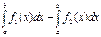 г) якщо функція y= f(x) на відрізку [a;b] декілька раз змінює знак, то
г) якщо функція y= f(x) на відрізку [a;b] декілька раз змінює знак, то
S= 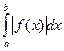
А) 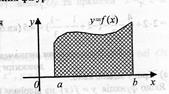 б)
б) 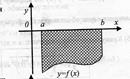
В) 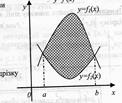
 приклад
приклад
Приклад. Обчислити площу фігури, обмеженої параболою y=x 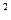 -2x і прямою y=2-x.
-2x і прямою y=2-x.
Знайдемо межі інтегрування, як абсциси точок перетину лінійy=x 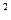 -2x і y=2-x: x
-2x і y=2-x: x 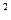 -2x =2-x; x
-2x =2-x; x 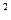 -x-2=0, x1=-1, x2=2
-x-2=0, x1=-1, x2=2
S= 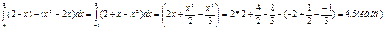
45) Застосування визначеного інтеграла для обчислення об*ємів та площ поверхонь тіл обертання
Якщо функція y= f(x) неперервна на відрізку [a;b], то об*єм тіла, яке утворене обертанням навколо осі Ox фігури, що обмежена графіком функції y= f(x), віссю Ox та прямими x=a, x=b обчислюється за формулою: V=π 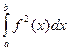 Аналогічно, об*єм тіла, яке утворене обертанням навколо осі Oy фігури, що обмежена графіком функції x= φ(y), віссю Oy та прямими x=c,x=d знаходяться за формулою: V=π
Аналогічно, об*єм тіла, яке утворене обертанням навколо осі Oy фігури, що обмежена графіком функції x= φ(y), віссю Oy та прямими x=c,x=d знаходяться за формулою: V=π 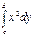 Приклад. Обчислити об*єм тіла,утвореного обертанням навколо осі Ox фігури, що обмежена лініями y=
Приклад. Обчислити об*єм тіла,утвореного обертанням навколо осі Ox фігури, що обмежена лініями y= 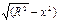 , y=0.Зобразимо фігуру, обмежену лініями y=
, y=0.Зобразимо фігуру, обмежену лініями y= 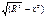 , y=0. При її обертанні отримуємо кулю радіаса R. Тоді об*єм куліV= π
, y=0. При її обертанні отримуємо кулю радіаса R. Тоді об*єм куліV= π  π
π 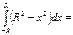 π
π 
 πR
πR  Отримали відому формулу для обчислення об*єму кулі.
Отримали відому формулу для обчислення об*єму кулі.
Якщо функція y= f(x) у кожній внутрішній точці відрізка [a;b] має неперервну похідну f’(x), то площу поверхніб яка отримується при обертанні графіка функції y= f(x) (a<=x<=b) навколо осі Ox, визначають за формулою Sn=2 π 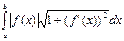
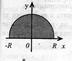
46)Інтеграл "першого роду" на необмеженій області визначення Нехай 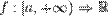 та
та 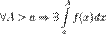 .Тоді:Якщ
.Тоді:Якщ 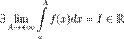 , то використовується позначення
, то використовується позначення  та інтеграл називається невластивим інтегралом Рімана першого роду. В цьому випадку
та інтеграл називається невластивим інтегралом Рімана першого роду. В цьому випадку 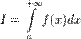 називається збіжним.Якщо
називається збіжним.Якщо 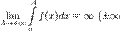 або
або 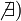 , то в цьому випадку інтеграл називається розбіжним до
, то в цьому випадку інтеграл називається розбіжним до 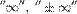 , чи просто розбіжним.Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:1) відрізок інтегрування [а, b] скінчений; 2) підінтегральна функція f(x) неперервна або обмежена і має скінченну кількість точок розриву. Якщо хоч би одна із умов не виконується, то визначений інтеграл називають невласним.Якщо не виконується перша умова, тобто b = ∞ або а = ∞ або а = -∞ та b = ∞, то інтеграли називають невласними інтегралами з нескінченними межами.Якщо не виконується лише друга умова, то підінтегральна функція f(x) має точки розриву другого роду на відрізку інтегрування [а, b]. В цьому випадку
, чи просто розбіжним.Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:1) відрізок інтегрування [а, b] скінчений; 2) підінтегральна функція f(x) неперервна або обмежена і має скінченну кількість точок розриву. Якщо хоч би одна із умов не виконується, то визначений інтеграл називають невласним.Якщо не виконується перша умова, тобто b = ∞ або а = ∞ або а = -∞ та b = ∞, то інтеграли називають невласними інтегралами з нескінченними межами.Якщо не виконується лише друга умова, то підінтегральна функція f(x) має точки розриву другого роду на відрізку інтегрування [а, b]. В цьому випадку 
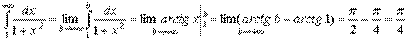
47) Нехай функція 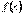 визначена і неперервна при
визначена і неперервна при 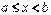 , а в точці
, а в точці 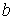 вона або невизначена, або має розрив другого роду. Тому говорити про інтеграл
вона або невизначена, або має розрив другого роду. Тому говорити про інтеграл 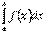 як про границю інтегральної суми неможливо, тому що функція
як про границю інтегральної суми неможливо, тому що функція 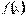 не є неперервною на відрізку
не є неперервною на відрізку 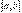 і, внаслідок цього, границя інтегральної суми, в класичному розумінні, не може існувати. Означення 1. Якщо існує скінчена лівостороння границя
і, внаслідок цього, границя інтегральної суми, в класичному розумінні, не може існувати. Означення 1. Якщо існує скінчена лівостороння границя 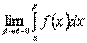 , то цю границю називають невласним інтегралом від розривної функції на відрізку
, то цю границю називають невласним інтегралом від розривної функції на відрізку  і вважають, що
і вважають, що 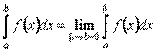 . (8.2.1)У цьому випадку інтеграл називають збіжним, а саму функцію
. (8.2.1)У цьому випадку інтеграл називають збіжним, а саму функцію 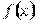 інтегрованою на відрізку
інтегрованою на відрізку  . Якщо границя рівна
. Якщо границя рівна 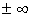 , або зовсім не існує, то інтеграл розбіжний.Аналогічно визначається невласний інтеграл другого роду, якщо функція неперервна при
, або зовсім не існує, то інтеграл розбіжний.Аналогічно визначається невласний інтеграл другого роду, якщо функція неперервна при 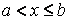 , а в точці
, а в точці  вона або невизначена, або має розрив другого роду:
вона або невизначена, або має розрив другого роду: 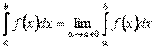 . (8.2.2)Якщо ж функція має розрив в деякій точці
. (8.2.2)Якщо ж функція має розрив в деякій точці 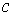 , яка лежить всередині відрізка
, яка лежить всередині відрізка  , то, згідно означення, вважають, що
, то, згідно означення, вважають, що 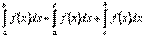 , (8.2.3)якщо два інтеграли, що лежать в правій частині існують
, (8.2.3)якщо два інтеграли, що лежать в правій частині існують
48)Диференціальні рівняння в частинних похідних — це рівняння, що містять невідомі функції від декількох змінних та їх частинних похідних.Загальний вид таких рівнянь можна представити у вигляді: 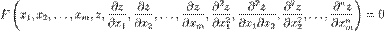 ,де
,де 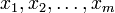 — незалежні змінні, а
— незалежні змінні, а 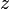 — функція цих змінних.Не лінійні диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування нелінійних рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні нелінійні диференціальні) чи кількох аргументів (нелінійні диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.Диференційні рівняння Загальний розв'язок 1
— функція цих змінних.Не лінійні диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування нелінійних рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні нелінійні диференціальні) чи кількох аргументів (нелінійні диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.Диференційні рівняння Загальний розв'язок 1 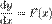
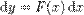
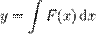 2
2 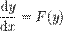
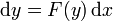
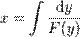 3
3 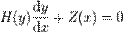
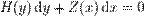
 4
4 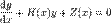
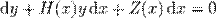
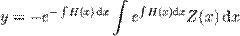 5
5 
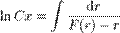
розв'язком може бути неявна фунція від x тa y, отримана обчисленням наведеного інтегралу використовуючи заміну змінних 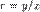
49) Лінійне диференціальне рівняння 1-го порядку зі змінними коефіцієнтами має загальний вигляд 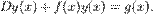 Тут D - диференціальний оператор. Рівняння такого виду може бути розв'язане множенням на інтегруючий множник
Тут D - диференціальний оператор. Рівняння такого виду може бути розв'язане множенням на інтегруючий множник  ,що дає
,що дає 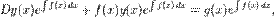 спрощуючи за правилом добутку, дістанемо
спрощуючи за правилом добутку, дістанемо 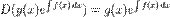 Звідси інтегруванням
Звідси інтегруванням 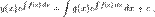
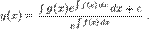 Отже, розв'язком лінійного диференціального рівняння першого порядку
Отже, розв'язком лінійного диференціального рівняння першого порядку 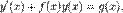 з коефіцієнтами, які можуть залежати від х, є:
з коефіцієнтами, які можуть залежати від х, є: 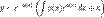 Зазначимо, що
Зазначимо, що  - стала інтегрування, і
- стала інтегрування, і  Компактна форма загального розв'язку
Компактна форма загального розв'язку  Розглянемо диференціальне рівняння першого порядку із сталими коефіцієнтами:
Розглянемо диференціальне рівняння першого порядку із сталими коефіцієнтами:  Це рівняння має особливе значення для систем першого порядку на кшталт RC-схем (ємність-опір) і систем маса-демпфер.В цьому випадку f(х) = b, g(х) = 1. Тож розв'язком є
Це рівняння має особливе значення для систем першого порядку на кшталт RC-схем (ємність-опір) і систем маса-демпфер.В цьому випадку f(х) = b, g(х) = 1. Тож розв'язком є 
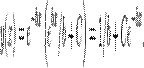
50) Рівняння виду у' = f(х) 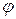 (у). (7)де y(х) і
(у). (7)де y(х) і 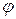 (у) — задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.Права частина рівняння (7) являє собою добуток двох множників, кожен з яких є функцією лише однієї змінної. Щоб розв'язати рівняння (7), треба відокремити змінні.Для цього замінимо у' на
(у) — задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.Права частина рівняння (7) являє собою добуток двох множників, кожен з яких є функцією лише однієї змінної. Щоб розв'язати рівняння (7), треба відокремити змінні.Для цього замінимо у' на 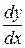 , поділимо обидві частини рівняння (7) та
, поділимо обидві частини рівняння (7) та 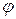 (у) (вважаємо, що
(у) (вважаємо, що 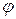 (у)
(у)  0) і помножимо на dx, тоді рівняння (7) запишеться у вигляді
0) і помножимо на dx, тоді рівняння (7) запишеться у вигляді 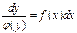 (8)Диференціальне рівняння виду (8), в якому множник при dx є функцією, яка залежить лише від х, а множник при dy є функцією, яка залежить лише від у, називається диференціальним рівнянням з відокремленими змінними.(х + хуг) dx-(y + ухг) dy = 0.Оскільки це рівняння можна записати у вигляді х (1+ y2)dx-у( 1+ x2)dy = 0, то воно є рівнянням з відокремлюваними змінними. Поділивши обидві його частини на (1 + х2) (1 + у2)
(8)Диференціальне рівняння виду (8), в якому множник при dx є функцією, яка залежить лише від х, а множник при dy є функцією, яка залежить лише від у, називається диференціальним рівнянням з відокремленими змінними.(х + хуг) dx-(y + ухг) dy = 0.Оскільки це рівняння можна записати у вигляді х (1+ y2)dx-у( 1+ x2)dy = 0, то воно є рівнянням з відокремлюваними змінними. Поділивши обидві його частини на (1 + х2) (1 + у2)  0, дістанемо рівняння з відокремленими змінними:
0, дістанемо рівняння з відокремленими змінними:  або
або 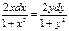 Інтегруючи останнє рівняння, маємо ln(l+ х 2) = ln(l + у 2) + ln|C|, С
Інтегруючи останнє рівняння, маємо ln(l+ х 2) = ln(l + у 2) + ln|C|, С  О. Потенціюючи, дістаємо загальний інтеграл заданого рівняння:
О. Потенціюючи, дістаємо загальний інтеграл заданого рівняння:
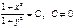
51) 51)* Лінійне диференційне рівняння зі сталими коефіцієнтами - диференційне рівняння виду 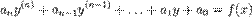 ,де коефіцієнти
,де коефіцієнти 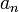 - певні сталі,
- певні сталі, 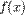 - довільна функція.Однорідне лінійне диференційне рівняння зі сталими коефіцієнтами
- довільна функція.Однорідне лінійне диференційне рівняння зі сталими коефіцієнтами 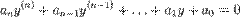 .Розв'язки однорідного лінійного диференціального рівняння зі сталими коефіцієнтами шукаються у вигляді
.Розв'язки однорідного лінійного диференціального рівняння зі сталими коефіцієнтами шукаються у вигляді 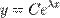 ,де
,де 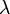 - комплексне число. Підстановка цієї пробної функції в рівняння дає характеристичне рівняння
- комплексне число. Підстановка цієї пробної функції в рівняння дає характеристичне рівняння  .Характеристичне рівняння є алгебраїчним рівнянням n-го степеня і має n у загальному випадку комплексних розв'язків. Якщо серед розв'язків немає кратних, то функції
.Характеристичне рівняння є алгебраїчним рівнянням n-го степеня і має n у загальному випадку комплексних розв'язків. Якщо серед розв'язків немає кратних, то функції 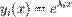 ,є лінійно-незалежними і загальний розв'язок однорідного диференційного рівняння записується у вигляді
,є лінійно-незалежними і загальний розв'язок однорідного диференційного рівняння записується у вигляді 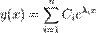 ,де
,де 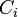 - довільні сталі
- довільні сталі
52) Диференціальне рівняння є лінійним, якщо воно має вигляд y’+p(x)y=q(x), де p (x) і q(x)- відомі функції.
Якщо q(x), то диф. р-ня є лінійним однорідним. Теорема. Загальний розв*язок неоднорідного лінійного диференціального р-ня дорівнює сумі частинного розв*язку неоднорідного і загального розв*язку однорідного диф р-ня:y 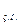 =y
=y 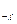 +y
+y 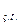 Для розв*язання лінійних диф р-нь використовують метод Лагранжа варіації довільної сталої6
Для розв*язання лінійних диф р-нь використовують метод Лагранжа варіації довільної сталої6
1) знайти розв*язок однорідного р-ня y’+p(x)y=0, де входить довільна стала. Загальним розв*язком однорідного р-ня є
y = Ce  , де С- стала.2) знайти розв*язок неоднорідного р-ня увигляді розв*язку однорідного р-ня, де довільну сталу розглядаємо, як нову шукану функцію C(x): у= C(x)е
, де С- стала.2) знайти розв*язок неоднорідного р-ня увигляді розв*язку однорідного р-ня, де довільну сталу розглядаємо, як нову шукану функцію C(x): у= C(x)е 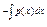 (*)
(*)
Підставляючи замість у і у’ в задане диф р-ня відповідні вирази, дістанемо для невідомої функції C(x) р-ня з відокремленими змінними, звідки і знаходимо C(x): C(x)= 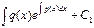 , де С
, де С 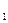 -стала
-стала
3) Підставляючи замість C(x) одержаний вираз в формулу (*), знаходимо загальний розв*язок заданого р-ня: у=е 
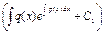 Приклад. З найти загальний розв*язок р-ня xy’+y=3x
Приклад. З найти загальний розв*язок р-ня xy’+y=3x 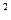 1) розв*яжемо відповідне однорідне лінійне р-ня: xy’+y=0, y’+
1) розв*яжемо відповідне однорідне лінійне р-ня: xy’+y=0, y’+ 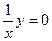 Використаємо формулу y = Ce
Використаємо формулу y = Ce  :y = Ce
:y = Ce 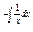 ,у= Ce
,у= Ce 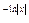 , у=Cx
, у=Cx 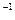 , у=
, у= 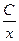 . 2) знайдемо розв*язок неоднорідного р-ня у вигляді у=
. 2) знайдемо розв*язок неоднорідного р-ня у вигляді у= 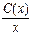 y’=
y’= 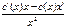
Підставивши в р-ня xy’+y=3x 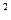 з амість y’ та y відповідні вирази, дістанемо x
з амість y’ та y відповідні вирази, дістанемо x 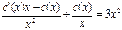 ,
, 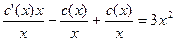 , c’(x)=3x
, c’(x)=3x 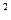 ,c(x)=
,c(x)= 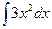 , c(x)=x
, c(x)=x  +c
+c 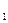 3) загальний розв*язок даного р-ня: у=
3) загальний розв*язок даного р-ня: у= 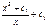 , де с
, де с 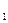 -стала
-стала
Не нашли, что искали? Воспользуйтесь поиском: