
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Частинні похідні. приклади. геометричний зміст
В математиці, часткова похідна (частинна похідна) функції кількох змінних — це похідна по одній із змінних, причому інші змінні приймаються як константи. Часткові похідні використовуються у векторному численні та диференційній геометрії.Часткова похідна функції f за змінною x записується так: fx або ∂f/∂x. Символ часткової похідної ∂ — це заокруглена форма літери d, що використовувалась для запису повної похідної. Позначення було запропоноване Лежандром і стало використовуватись після його представлення в працях Якобі.Означення  Нехай f — функція, що залежить більш ніж від однієї змінної. Наприклад,
Нехай f — функція, що залежить більш ніж від однієї змінної. Наприклад, 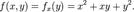 Тут f можна інтерпретувати як родину функцій від однієї змінної при заіндексованій іншій:
Тут f можна інтерпретувати як родину функцій від однієї змінної при заіндексованій іншій: 
 Іншими словами, при виборі нового значення x утворюється нова функція fx, котра є функцією від одного дійсного аргумента. Тобто,
Іншими словами, при виборі нового значення x утворюється нова функція fx, котра є функцією від одного дійсного аргумента. Тобто,  Припустимо, що значення x вибрано, покладемо його a, тоді f(x,y) визначає функцію fa, залежну тільки від y: a² + ay + y²:
Припустимо, що значення x вибрано, покладемо його a, тоді f(x,y) визначає функцію fa, залежну тільки від y: a² + ay + y²: 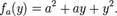 В цьому виразі, a - константа, а не змінна, отже fa - функція від одного дійсного аргумента - y. Відповідно до означення похідної функції одного аргумента:
В цьому виразі, a - константа, а не змінна, отже fa - функція від одного дійсного аргумента - y. Відповідно до означення похідної функції одного аргумента:  Наведену процедуру можна здійснити для довілього вибору a. Узагальнивши всю сім'ю функцій, отримаємо похідну функції f по змінній y:
Наведену процедуру можна здійснити для довілього вибору a. Узагальнивши всю сім'ю функцій, отримаємо похідну функції f по змінній y:  Тут використовується символ ∂, котрий називають символом часткової похідної.В загальному випадку, часткову похідну функції f(x1,...,xn) за змінною xi в точці (a1,...,an) записують так:
Тут використовується символ ∂, котрий називають символом часткової похідної.В загальному випадку, часткову похідну функції f(x1,...,xn) за змінною xi в точці (a1,...,an) записують так:  В цьому різницевому відношенні усі змінні, крім xi, зафіксовані. Іншими словами, різний вибір індекса a приводить до утворення родини функцій як у наведеному прикладі. Цей приклад також показує, що обчислення часткової похідної, в обчислювальному сенсі, простіше, ніж повної похідної.
В цьому різницевому відношенні усі змінні, крім xi, зафіксовані. Іншими словами, різний вибір індекса a приводить до утворення родини функцій як у наведеному прикладі. Цей приклад також показує, що обчислення часткової похідної, в обчислювальному сенсі, простіше, ніж повної похідної.
Важливим прикладом функції кількох змінних є випадок скалярної функції f(x1,...xn) в евклідовому просторі Rn (наприклад, R² або R³). В цьому випадку f має часткову похідну ∂f/∂xj по кожній змінній xj. В точці a, ці часткові похідні визначають вектор  Цей вектор називають градієнтом f в точці a. Якщо f диференційовна в кожній точці певної області, то градієнт — векторна функія ∇f, котра в точці a перетворюється у вектор ∇f(a). Відповідно градієнт визначений у векторному полі. Приклади Припустимо V — об'єм конуса; він залежиить від висоти h та радіусу r за формулою
Цей вектор називають градієнтом f в точці a. Якщо f диференційовна в кожній точці певної області, то градієнт — векторна функія ∇f, котра в точці a перетворюється у вектор ∇f(a). Відповідно градієнт визначений у векторному полі. Приклади Припустимо V — об'єм конуса; він залежиить від висоти h та радіусу r за формулою 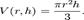 часткова похідна об'єму V за радіусом r буде
часткова похідна об'єму V за радіусом r буде 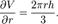 Вона описує, як змінюється об'єм конуса від зміни радіуса при сталій висоті. Часткова похідна за висотою h
Вона описує, як змінюється об'єм конуса від зміни радіуса при сталій висоті. Часткова похідна за висотою h  і вона показує, як змінюється об'єм конуса при зміні висоти та сталому радіусі.Тепер для порівняння знайдемо повні похідні V за змінними r та h. Вони, відповідно, мають вигляд
і вона показує, як змінюється об'єм конуса при зміні висоти та сталому радіусі.Тепер для порівняння знайдемо повні похідні V за змінними r та h. Вони, відповідно, мають вигляд 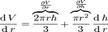 Та
Та 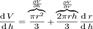
Не нашли, что искали? Воспользуйтесь поиском: