Прямокутна декартова система координат на площі та у просторі.

Числовою віссю називають пряму на якій визначено напрям початок відліку та одиничний відрізок.

Координатою точки М на осі називають відстань ОМ від цієї точки до початку відліку що береться зі знаком + якщо точка лежить на додатнй півосі, зі знаком «-» якщо вона лежить на відємній півосі

Дві взаємно перпендикулярні числові осі зі спільним початком відліку називають прямокутною декартовою системою координат.Горизонтальну вісь називають віссю абсцис, а вертикальну-вссю ординат. Точка перетину – початок координат.

Числа х і у однозначно визначають положення точки М на площині і називають координатами точки х- абсцисою, у- ординатою точки М.Осі координат розбивають площину на 4 частини які називають координатними чвертями.

Три взаємно перпендикулярні числові осі зі спльним початком відліку називають прямокутною системою координат у просторі.Вісь ОХ- вісь абсцис, ОУ- вісь ординат,OZ- вісь аплікат.Числа х,у та z координати проекції точки М на осі абсцис, ординат та аплікат однозначно визначають положення точки М у просторі називають координатами точки М і записують М (х у z) Поняття рівняння лінії на площині. Види рівнянь прямої на площині

Рівнянням лінії l на площині називають рівняння F (x,y)=0 із змінними х задовольняють координати довільної точки М(х,у) цієї лінії і не задовольняють координати будь – якої точки,що не належать лінії l. Найпростішою лінією на площині є пряма. Види рівнянь прямої на площині.Загальним рівнянням прямої на площині називається рівняння 1-го степеня відносно х та у вигляду Ах+Ву +С =0 де А,В,С – сталі числа при чому А і В не дорівнюють 0.Частинні випадки загального рівняння прямої: Ах+ Ву=0 – пряма проходить через початок координат. Ву + С =0 – пряма паралельна осі ОХ.Ах +С=0 – пряма паралельна осі ОУ.У=0 – вісь ОХ.Х=0 – Вісь ОУ

15 Прямокутна таблиця,складена із довільного набору величин,називається прямокутною матрицею. Величини з яких вона складається-елементи матриці.Матриці позначаються великими латинськими літерами,її елементи-малими ї двома індексами(перший-номер рядка,другий-номер стовпця).

Добуток числа рядків m начисло стовпців n наз. розміром матриці(m×n)Види матриць:1.Квадратна-кількість рядків і стовпців рівна.Кількість їх-це порядок.2.Нульова-квадратна матриця,всі елементи дорівнюють 0.3.Діагональна- квадратна матриця,всі елементи якої крім діагональних дорівнюють 0.4.Одиночна-діагональна матриця всі елементи головної діагоналі якої дорівнюють 1.5.Матриця рядок(стовпець)-матриця яка складається з одного рядка (стовпця).6.Трикутна-всі елементи якої розміщенні під головною діагоналлю дорівнюють 0.7.Транспонована-матриця в якої після перетворень рядки стали стовпцями.Дії над ними:1.Додавання(віднімання).Сумою(різницею)2 матриць А і В однакових розмірів наз. Матриця С такого ж розміру кожний елемент якої дорівнює сумі (різниці) відповідних елементів.2.Множення матриці на число.кожний елемент матриці потрібно помножити на дане число.3)Добуток матриць. Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m -на- n (m рядків, n стовпчиків), а B — матриця n -на- p (n рядків, p стовпчиків), їх добуток AB є матрицею m -на- p (m рядків, p стовпчиків), що розраховується за формулою: Властивості:

1.1A=A 8.k(A+B)=kA+kB

2.0A=0 9.A+0=A

3.k0=0 10.A(B+C)=AB+AC

4.A+B=B+A 11.(A+B)C=AC+BC

5.k(lA)=(kl)A=l(kA) 12.k(AB)=(kA)B=A(kB)

6.A+(B+C)=(A+B)+C 13.A(BC)=(AB)C

7.(k+l)A=kA+LA 14.AE=EA=AОсобливості:1.Якщо добуток АВ існує то добуток ВА може не існувати.2.Переставна властивість справджується не завжди.Якщо А×В=В×А,то матриці наз. Переставними(комутативними).

3.З рівності АВ=0 не випливає, що А=0 або В=0

16) Число що ставиться у відповідність матриці наз. її визначником.

Матричний метод.

1.Позначаєм матрицю як А. В-матриц- стовпець з вільних членів

2.матрицю-стовпець з невідомих

3.сиистему лінійних рівнянь записуєм у формі АХ=В

4.Матричний розв’язок буде Х=А^-1В

5.Обчислюєм визначник А,якщо він не дорівнює 0 то можна знайти А^-1.

6.Знаходим алгебриїчні доповнення елементів матриці А.

7.будуєм транспоновану матрицю.

Множим транспоновану матрицю на А^-1.

\

18. Метод Крамера

Спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році.

1.Знаходим Δ за методом трикутників.

2.знаходим ΔХ,для цього замість першого стовпця підставляєм ставимо стовпець В

3.знаходимо ΔУ,замість 2-го стовпця ставимо В

4.знах. ΔZ,замість 3-го ставимо В

5.для знаходження Х ділимо ΔХ на Δ,для У- Δ У/ Δ,для Z- ΔZ/ Δ/

Метод Гауса.

1.Вибираєм ведуче рівняння,біля А11 має бути 1.Якщо ні то ділим на А11

2.домножаєм ведуче на А21.

3.від 2-го р-ння віднімаєм те що вийшло.

4.домножаєм ведуче на А31

5.від 3-го віднімаєм не що вийшло

6.зводим ведуче, те що вийшлоу 3 операції і те що у 5.

7.якщо матриця трикутної форми розвязуєм,якщо ні застосовуєм елементарні перетворення

20)Функціональна залежність (далі часто ФЗ) —Математично являє собою бінарне відношення між множинами атрибутів даного відношення і є, по суті, зв'язком типу «один-до-багатьох. Функціональна залежністьНехай маємо відношення зі схемою (заголовком) , і — деякі підмножини множини атрибутів відношення . Множина функціонально залежить від тоді і тільки тоді, коли кожне значення множини зв'язане точно з одним значенням множини . Іншими словами, якщо два кортежі збігаються за атрибутами , то вони збігаються і за атрибутами .

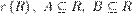
У такому разі — детермінант, — залежна частина.ФЗ називається тривіальною, якщо залежна частина є підмножиною детермінанта.

Замикання множини залежностей.Одні функціональні залежності можуть припускати інші функціональні залежності. Наприклад, Множина всіх ФЗ, які припускаються даною множиною ФЗ називається замкненням множини .

Поняття функції.Означення. Якщо кожному елементу х множини х (х є х) за деяким законом ставиться у відповідність певний елемент у множини у (у є у), тоді говорять, що на множині х задано функцію у = f(x).Змінну величину х називають незалежною змінною або аргументом, у – незалежною, а літера f позначає закон відповідності.Множина х називається областю визначення функції, а множина у – областю значень функції.Якщо множина у спеціально не вказано, то під областю визначення функції вважатимемо множину таких значень х, при яких функція у= f(х) взагалі має зміст. Наприклад Областю визначення функції у = х² + є пів інтервал , оскільки 5 – х 0.Існує кілька способів здання функції. Найпоширеніші серед них такі.1. Аналітичний спосіб: якщо функцію задано формулою вигляду у = f(х). Так, функцію у = х² + задано аналітично.2. Табличний спосіб: полягає в тому, що функція задається таблицею, яка містить значення аргументу х і відповідні значення функції f(х). Наприклад, таблиця синусів або косинусів.3. Графічний спосіб: полягає у зображенні рафіка функції – множини точок (х, у) площини, абсциси яких є значенням аргументу х, а ординати – відповідні їм значення функції у = f(х). При цьому способі функціональна залежність зображується лінією, яку називають графіком функції.Якщо рівняння, що зв’язує аргумент х з функцією у, не розв’язано відносно у, а задано у вигляді f(х, у) = 0, тоді змінну у називають неявною функцією х, (наприклад, 3х – 7у = 6).1. Парність і непарність: Функція у = називається парною, якщо для будь-яких значень х із області визначення = , і непарною, якщо = - . В іншому випадку функція у = називається функцією загального вигляду. Наприклад функція у = х² є парною, оскільки = (-х)² = х² і = , а функція у = х³ – непарною, оскільки = (-х)³ = - х³ і = - .

Крім того, функція у = х² + х³ є функцією загального вигляду, оскільки = (-х)² + (-х)³ = х² - х³,

і - .Графік першої функції симетричний відносно осі ординат, а графік непарної функції симетричний відносно початку координат.2. Монотонність: Функція у = називається зростаючою (спадною) на проміжку х, якщо більшому значенню аргументу з цього проміжку відповідає більше (менше) значення функції.

Нехай х₁, х₂ х і х₂ > х₁. Тоді функція зростає на проміжку х, якщо > , і спадає, якщо < . Зростаючі і спадні функції називають монотонними. Так, функція у = х² при х [- 0] спадає і при х [0, ] зростає.3. Обмеженість: Функція називається обмеженою на проміжку х, якщо існує таке додатне число М>0, що £ М для будь-якого х Х. Наприклад функція у = sin x обмежена на всій числовій осі, оскільки £1 для будь-якого х Х.4. Періодичність: Функція у = називається періодичною з періодом Т 0, якщо для будь-яких х із області визначення функцій = . Наприклад функція у = sin x має період Т=2 , оскільки для будь-яких sin x. Найменше додатне число Т, що задовольняє цю рівність, називається періодом функції. Основні елементарні функції:1Степенева функція вигляду у = хⁿ, де n – дійсне число. Показникові функція вигляду у = а^х, де а>0, а 1. Логарифмічна функція у = log_a х, де а>0, а 1. Тригонометричні функції у = sin x; у = соs х; у = tg х; у = ctg х. Обернені тригонометричні функції у = arcsin х; у = arcos х; у = arctg х; у = arcctg х. Якщо змінна у залежить від другої змінної величини И, яка у свою чергу є функцією х, то у називають функцією від функції або складною функцією.Математично це можна записати так:якщо у = , u = 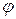(х), то у = .у – складна функція х; u – проміжний аргумент; х – аргумент (незалежна змінна). Наприклад: у = соs³ х, або у = u³, де u = соs х.Функції, побудовані з основних елементарних функцій з допомогою скінченого числа алгебраїчних дій і скінченого числа операцій утворення складної функції, називаються елементарними.Елементарні функції розподіляються на алгебраїчні і неалгебраїчні (трансцендентні). Алгебраїчною називається функція, в якій над аргументом проводиться скінчене число алгебраїчних дій.До алгебраїчний функцій належать:ціла раціональна функція (многочлен) - дробово-раціональна функція – відношення двох многочленів;- ірраціональна функція – якщо в складі операцій над аргументом ї здобуття кореня.Будь-яка неалгебраїчна функція називається трансцендентною.До неалгебраїчних функцій належать: показникова;логарифмічна;тригонометрична;обернені тригонометричні функції.

20,3 Область визначення — множина допустимих значень аргументу функції. Позначається як D(y), якщо вказується область визначення функції y=f(x).

Якщо задані: числова множина та правило 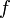, що дозволяє поставити у відповідність кожному елементу з множини певне число, то говорять, що задана функція з областю визначення .

Тобто, визначення області значень є необхідною умовою визначення функції.

Визначення. Значення змінних, на яких задається функція , називають допустимими значеннями змінних.

Визначення. Значення змінних, при яких алгебраїчний вираз має зміст, називають допустимими значеннями змінних. Множину всіх допустимих значень змінних називають областю допустимих значень змінних .

Визначення. Областю визначення рівняння називають множину всіх тих значень зміної , при яких алгебраїчні вирази і одночасно мають зміст.

Якщо функція задана формулою, то область визначення складається зі всіх значень незалежної змінної, при яких формула має зміст.

Приклади

Нижче наведені умови на області визначення алгебраїчних виразів від деяких елементарних функцій дійсного аргумента

Функція	Область визначення функції

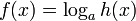
Областю значень функції (відображення) називається множина B ⊂ Y така, що f(X) = B.

Множина Y зовсім не обов'язково збігається з областю значень f. У загальному випадку, B є лише підмножиною Y.

Ред.]Приклад

Візьмімо функцію f, визначену на множині дійсних чисел:

де

Формально, відображення переводить R в R, але насправді f(x) ніколи не буде від'ємне, тому область значень є лише R ⁺ — тобто інтервалом [0,∞):

Не нашли, что искали? Воспользуйтесь поиском: