Дифференциал функции

Пусть функция 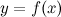дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно и нелинейного членов:

где при .

Определение

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:

Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Замечание

Формулу для дифференциала функции можно записать в виде:

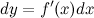
Отсюда получаем, что

Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.

Не нашли, что искали? Воспользуйтесь поиском: