Образец выполнения задания №4

Задача 1. Вероятность того, что на некотором предприятии расход электроэнергии не превысит суточной нормы, равна 0,75. Какова вероятность того, что из пяти проверенных дней расход электроэнергии не превысит суточную норму: а) три дня? б) хотя бы один рабочий день? в) не менее 2 дней?

Решение. Производится 5 независимых испытаний. Каждое испытание имеет два исхода: расход электроэнергии не превысит норму, расход электроэнергии превысит норму. Вероятность не превышения нормы расхода электроэнергии в каждом испытании постоянна и равна 0,75, т.е. p =0,75. Таким образом, мы имеем дело со схемой Бернулли. Для нахождения искомых вероятностей применим формулу Бернулли и её следствия

а) Здесь n=5, m=3, p=0,75, q=1-p=0,25. Отсюда

.

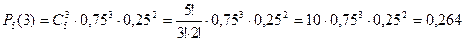б) Искомая вероятность равна

.

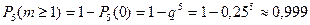в) Искомая вероятность равна

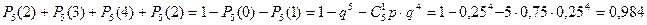Ответ: а) P =0,264; б) P =0,999; в) P =0,984.

Задача 2. Некто приобрел 200 билетов лотереи. Известно, что вероятность выигрыша на один билет лотереи равна 0,01. Какова вероятность того, что среди приобретенных выигрышных билетов окажется: а) два? б) хотя бы два? в) 3 или 4?

Решение. По условию задачи имеем n =200, p =0,01. Поскольку n -достаточно велико, p -мало, но a = пр =2<10, то для вычисления искомых вероятностей можно воспользоваться формулой Пуассона

а)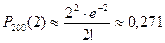

б)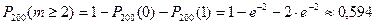

в)

Ответ: а) P =0,271, б) P =0,594, в) P =0,271;

Задача 3. Из ящика, в котором 20 белых и 4 черных шара, 100 раз извлекается по одному шару, причем после каждого извлечения шар возвращается. Найдите вероятность того, что черный шар извлечен: а) 15 раз; б) не более 40 раз и не менее 15 раз.

Решение. По условию задачи имеем n =100, -вероятность извлечь черный шар в каждом испытании. Поскольку n -велико и пр = 20>10, то для вычисления искомых вероятностей удобно воспользоваться локальной и интегральной формулами Лапласа.

а) Так как , , то

б)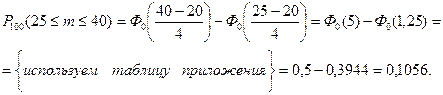

Ответ: а) Р =0,046, б) P =0,1056

Не нашли, что искали? Воспользуйтесь поиском: